带有非期望产出的SBM模型(slacks-based measure)可用于处理多个投入和产出变量的效率测度问题,可用于工业经济绿色发展效率的分析。在绿色发展分析中,需要同时考虑经济收益(期望产出)和负面环境效应(非期望产出)的问题,一方面要提高经济收益,另一方面需要减少污染排放,是投入、期望产出和非期望产出三方权衡的问题。1
这个帖子记录了和非期望产出SBM模型苦苦斗争一个星期的学习成果。
数学原理
DEA模型/CCR模型
DEA
SBM模型是数据包络分析(Data Envelopment Analysis, DEA)的一种。在DEA模型中,假定存在$n$个可比决策单元(decision making units, DMU),记为$DMU_j(j=1,2,\dots,n)$;
每个$DMU$有$m$种投入,记为$X_i(i=1,2,\dots,m)$,每种投入的权重为$v_i$;
有$q$种产出,记为$Y_r(r=1,2,\dots,q)$,每种产出的权重为$u_r$.
对第$k$个可比决策单元而言,其投入产出比(技术效率)为
$$ H_k=\frac{\sum_{r=1}^qu_rY_{rk}}{\sum_{i=1}^mv_iX_{ik}}, $$
限定范围为$H_k\in[0,1]$. 现要求在所有可比决策单元的效率均不超过$1$的条件下,调节权重$[v_1,v_2,\dots,v_m]$和$[u_1,u_2,\dots,u_q]$,使得被评价的单元$DMU_k$效率值最大化。即如下规划模型: $$ \begin{aligned} \max&~~ z=\frac{\sum_{r=1}^qu_rY_{rk}}{\sum_{i=1}^mv_iX_{ik}}\\ s.t.&~~ \frac{\sum_{r=1}^qu_rY_{rj}}{\sum_{i=1}^mv_iX_{ij}}\le1~ (v_i\ge0,u_r\ge0)\\ &~~ i=1,2,\dots,m;~r=1,2,\dots,q;~j=1,2,\dots,n \end{aligned} $$
该模型所确定的权重系数组合是对于$DMU_k$最有利的。由于$\sum_{i=1}^mv_iX_{ik}>0$,模型的规划条件即为 $$ s.t.~~\sum_{r=1}^qu_rY_{rj}-\sum_{i=1}^mv_iX_{ij}\le0; $$
在上述线性规划模型中,所要求的是投入和产出项目的指标权重,在原始意义上就是$\vec u$和$\vec v$。模型指定了一个可比决策单元$DMU_k$,在规划过程中力求这个单元最终的效率评价达到最高。实际应用中,如何选择这个特殊的$DMU$必然会成为问题的关键。或许需要根据决策者的感性判断(或其他手段辅助),选定一个最优的决策单元,或者人为设置一个对照的“理想型”,将其视为效率最高的情形。
投入导向CCR
令$t=\left(\sum_{i=1}^mv_iX_{ik}\right)^{-1}$,则模型的目标函数为
$$ \max ~~ z=t\sum_{r=1}^qu_rY_{rk}=\sum_{r=1}^qtu_rY_{rk}, $$
令$\mu_{r}=tu_r, \nu_{i}=tv_i$,根据$t$的定义可知$\sum_{i=1}^m\nu_iX_{ik}=1$;将规划条件两边同乘$t$,得到
$$ s.t. ~~ \sum_{r=1}^q\mu_{r}Y_{rj}-\sum_{i=1}^m\nu_{i}X_{ij}\le0. $$
从而将非线性规划模型转换为线性规划模型:
$$ \begin{aligned} \max &~~ z=\sum_{r=1}^q\mu_{r}Y_{rk}\\ s.t. &~~ \sum_{r=1}^q\mu_{r}Y_{rj}-\sum_{i=1}^m\nu_{i}X_{ij}\le0~(\mu_r\ge0, \nu_i\ge0)\\ &~~ \sum_{i=1}^m\nu_iX_{ik}=1\\ &~~ i=1,2,\dots,m;~r=1,2,\dots,q;~j=1,2,\dots,n \end{aligned} $$
其对偶模型为(对偶模型求解过程见文末)
$$ \begin{aligned} \min & \theta=\sum_{j=1}^n\frac{X_{mj}}{X_{mk}}\lambda_j+\lambda_{n+1}\\ s.t. & \sum_{j=1}^n\lambda_jX_{ij}\le(\theta+\lambda_{n+1}) X_{ik}(\lambda_j\ge0)\\ & \sum_{j=1}^n\lambda_jY_{rj}\ge Y_{rk}\\ & i=1,2,\dots,m;r=1,2,\dots,q;j=1,2,\dots,n \end{aligned} $$
以上处理后得到的是投入导向的DEA模型。
这里与常见的处理方式有点差异,因为在转化为标准形式的时候规划模型的自由度减1。
产出导向CCR
同理,若在降低自变量自由度时采用$t=\left(\sum_{r=1}^qu_rY_{rk}\right)^{-1}$,则可演算得到产出导向的DEA模型:
$$ \begin{aligned} \min &~~ z=\sum_{i=1}^m\nu_{r}X_{ik}\\ s.t. &~~ \sum_{r=1}^q\mu_{r}Y_{rj}-\sum_{i=1}^m\nu_{i}X_{ij}\le0~(\mu_r\ge0, \nu_i\ge0)\\ &~~ \sum_{r=1}^q\mu_rY_{rk}=1\\ &~~ i=1,2,\dots,m;~r=1,2,\dots,q;~j=1,2,\dots,n \end{aligned} $$
其对偶模型为
$$ \begin{aligned} \min &~~ \phi=\sum_{j=1}^n\frac{Y_{qj}}{Y_{qk}}\lambda_j+\lambda_{n+1}\\ s.t. &~~ \sum_{j=1}^n\lambda_jY_{rj}\le(\theta+\lambda_{n+1}) Y_{rk}~~(\lambda_j\ge0)\\ &~~ \sum_{j=1}^n\lambda_jX_{ij}\ge X_{rk}\\ &~~ i=1,2,\dots,m;~r=1,2,\dots,q;~j=1,2,\dots,n \end{aligned} $$
SBM模型
不带非期望产出的情形
在DEA模型中,线性规划的最终目的是使得$H_k$尽可能大,即$DMU_k$的产出效率尽可能高。虽然考虑到了多种产出的情形,但是每一种产出的权重都是正的($u_r\ge0$) ,所以依然是要尽可能使得每一种产出都越高越好。当产出中存在非期望内容时,我们希望这些非期望的产出尽可能低,同时期望产出尽可能高。Kaoru Tone提出的SBM模型(slacks-based model)2可以处理这类非期望产出的问题。
我们仍然以$X=(x_{ij})\in R^{m\times n}$表示实际投入,$Y=(y_{rj})\in R^{q\times n}$表示实际产出。在不带非期望产出的情况下,有可能存在的生产情形必然包括投入更多、产出更低的情况(即效率更低的情况总是能够实现的):
$$ P=\left\{ \left(\vec x,\vec y\right) ~|~ \vec x\ge X\vec\lambda,~\vec y\le Y\vec\lambda,~\vec\lambda\ge\vec0 \right\} $$
其中$\vec\lambda$是$R^n$上的一个非负向量。
$X$矩阵的每一列代表了一个可比决策单元,当$X$右乘一个$n$维向量后得到的是一个$m$维向量,$X\vec\lambda=\left[ \sum_{j=1}^nx_{ij}\lambda_j \right]_{m\times1}$,可以视为由所有$DMU$按照$\vec \lambda$所规定的配比混合而成的新的生产投入组合。同理,$Y\vec\lambda$代表了所有$DMU$按照$\vec \lambda$所规定的配比混合而成的新的产出组合。$\left(X\vec\lambda, Y\vec\lambda\right)$就是所有实际生产情形线性混合而成的“虚拟生产情形”(基于规模报酬不变)。在这个“虚拟生产情形”的基础之上,更加浪费的生产情形必然是可行的,故采用上述形式定义有可能的生产情形。
在这种定义下,默认了效率最高的生产情形暗含在实际生产情形通过线性组合所形成的参数空间范围之中。即我们不考虑生产效率远远超出现有技术水平的情形。
具体地,用$(\vec x_0,\vec y_0)$来描述某一个$DMU_0$(从实际生产情形$X,Y$中而来): $$ \displaylines{ \vec x_0=X\vec\lambda + \pmb s^-\ \vec y_0=Y\vec\lambda - \pmb s^+ } $$ 其中$\pmb s^-\ge0,\pmb s^+\ge 0$分别称为投入过量(input excess)和产出不足(output shortfall),统一称为和投入和产出的松弛向量(slacks)。据此定义指标:
$$ \rho = \frac{1-\frac1m\sum_{i=1}^m\left({s^-_i}/{x_{i0}}\right)}{1+\frac1q\sum_{r=1}^q\left({s^+_r}/{y_{r0}}\right)} $$
该指标满足以下特性:
- 每个$DMU$都有一个不同的$\rho$
- 随着投入和产出松弛向量$\pmb s^-,\pmb s^+$而单调变化
- 取值范围为$\rho\in\left(0,1\right]$
为了表达$(\vec x_0,\vec y_0)$的效率,以$\rho$指标构建SBM模型:
$$ \begin{aligned} \min &~~\rho=\frac{1-\frac1m\sum_{i=1}^m\left({s^-_i}/{x_{i0}}\right)} {1+\frac1q\sum_{r=1}^q\left({s^+_r}/{y_{r0}}\right)}\\ s.t. &~~ \vec x_0 = X\vec\lambda + \pmb s^- \\ &~~ \vec y_0 = Y\vec\lambda - \pmb s^+\\ &~~ \vec\lambda\ge0,~\pmb s^-\ge0,~\pmb s^+\ge 0 \end{aligned} $$
当$DMU_0$达到效率最优(SBM-efficient)时,满足 $$ \rho^*=1,~\pmb s^-=0,~\pmb s^+=0 $$
如何理解$DMU$效率最优等同于松弛变量均为零?在作者的理解中,认为SBM-efficient意味着该决策单元的任何优化都不会引起投入过量和产出不足。
若有唯一的$\vec\lambda$,则确定唯一的$\left(\pmb s^-, \pmb s^+\right)\sim\left(\vec x_0,\vec y_0\right)$关系。规划自变量为$\left(\pmb s^-, \pmb s^+\right)$,目的是使得$\rho$尽可能小,即$\pmb s^-$和$\pmb s^+$都要尽可能大。这可以看成是一种对当下生产效率不信任的态度。
当处于效率最优状态时,生产投入的要素配比恰到好处,此时进行任何调节都无法使得效率进一步提升。
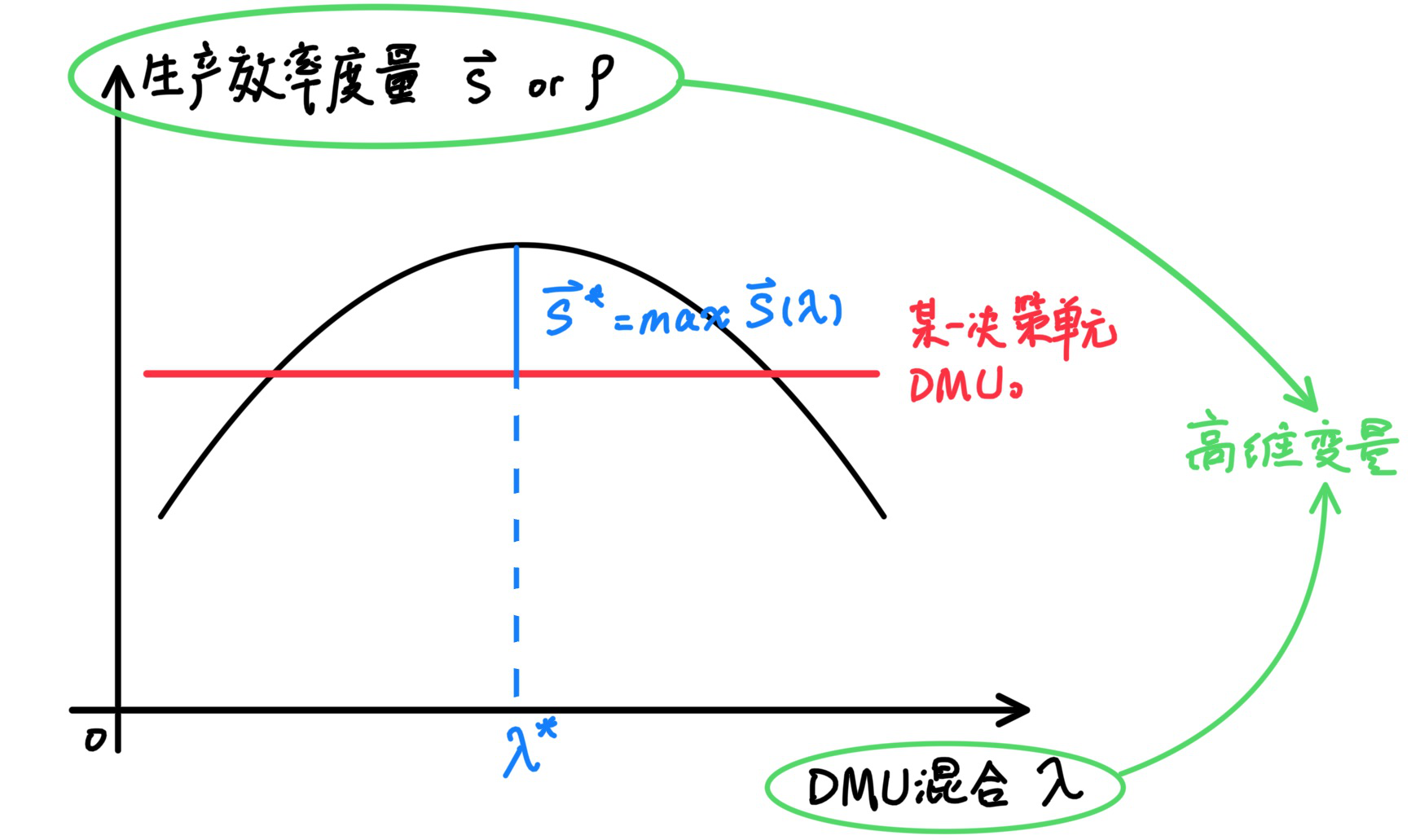
再将$\vec\lambda$也视为自变量,即尝试不同组合情况下的$DMU_0$,通过调整$\vec\lambda$可以进一步优化目标函数。
**Charnes-Cooper transformation: **将目标函数的分子和分母都乘$t$,使得分母变为$1$,即
$$ t=\left[1+\frac1q\sum_{r=1}^q\left(\frac{s^+_r}{y_{r0}}\right)\right]^{-1}, $$
从而目标函数变为
$$ \min~\rho=t-\frac1m\sum_{i=1}^m\frac{ts_i^-}{x_{i0}}. $$
定义$\pmb S^-=t\pmb s^-,\pmb S^+=t\pmb s^+,\pmb \Lambda=t\vec\lambda$,则原非线性规划中的约束条件转换为 $$ \begin{aligned} s.t. &~~ 1=t+\frac1q\sum_{r=1}^q\frac{S_r^+}{y_{r0}}\\ &~~ t\vec x_0=X\pmb \Lambda+\pmb S^-\\ &~~ t\vec y_0=Y\pmb \Lambda-\pmb S^+\\ &~~ \Lambda\ge0,\pmb S^-\ge0, \pmb S^+\ge0,t\ge0 \end{aligned} $$ 最后完整地写一下转换后的线性规划(多项式形式):
$$ \begin{aligned} \min &~~\rho=t-\frac1m\sum_{i=1}^m\frac{ts_i^-}{x_{i0}}\\ s.t. &~~ 1=t+\frac1q\sum_{r=1}^q\frac{S_r^+}{y_{r0}}\\ &~~ tx_{i0}=\sum_{j=1}^nx_{ij}\Lambda_j + S_i^- \\ &~~ ty_{r0}=\sum_{j=1}^n y_{rj}\Lambda_j-S_r^+ \\ &~~ \Lambda_j\ge0,S_i^-\ge0, S_r^+\ge0,t\ge0\\ &~~ i=1,2,\dots,m;r=1,2,\dots,q;j=1,2,\dots,n \end{aligned} $$
通过线性规划的可行解$\left(\rho^*,\vec\Lambda^*,t^*,\pmb S^{-*}, \pmb S^{+*}\right)$,可以解出原型的可行解$\left(\rho^*,\vec\lambda^*,\pmb s^{-*}, \pmb s^{+*}\right)$。
若$\rho^*=1$,则称该$DMU$为SBM-efficient,此时$\pmb s^{-*}=0,\pmb s^{+*}=0$; 若$\rho^*<1$,则称该$DMU$为SBM-inefficient,对于一个SBM-inefficient的决策单元(假设为$DMU_k$),其投入和产出满足:
$$ \displaylines{ \vec x_k = X\vec\lambda^* + \pmb s^{-*}\\ \vec y_k = Y\vec\lambda^* - \pmb s^{+*} } $$
由于得到了投入过量和产出不足的具体数值,因此我们可以对该可比决策单元进行优化,称为SBM投射(SBM-projection):
$$ \displaylines{ \vec x_k \leftarrow \vec x_k - \pmb s^{-*}\\ \vec y_k \leftarrow \vec y_k + \pmb s^{+*} } $$
带有非期望产出的情形
如果我们考虑到非期望产出的情形3,这些非期望产出在低效情况下的情形并非产出不足,而是“产出过多”,因此需要引入新的松弛向量$\pmb s^{+’}$以规范非期望产出。记$Y$为实际期望产出,$Z$为实际非期望产出,分别有$q_1,q_2$个。生产可能性中也应区分期望产出和非期望产出,即$(\vec x_0, \vec y_0,\vec z_0)$,其中 $$ \vec z_0=Z\vec\lambda + \pmb s^{+’}. $$ 同理以$\rho$指标构建SBM模型:
$$ \begin{aligned} \min &~~\rho=\frac{1-\frac1m\sum_{i=1}^m\left({s^-_i}/{x_{i0}}\right)} {1+\frac1{q_1+q_2}\left[\sum_{r_1=1}^{q_1}\left({s^+_r}/{y_{r0}}\right) + \sum_{r=1}^{q_2}\left({s^{+’}_r}/{z_{r0}}\right)\right]}\\ s.t. &~~ \vec x_0 = X\vec\lambda + \pmb s^- \\ &~~ \vec y_0 = Y\vec\lambda - \pmb s^+\\ &~~\vec z_0=Z\vec\lambda+\pmb s^{+’}\\ &~~ \vec\lambda\ge0,~\pmb s^-\ge0,~\pmb s^+\ge 0 \end{aligned} $$
当某一个$DMU$达到效率最优时,
$$ \rho^*=1,~\pmb s^-=0,~\pmb s^+=0,~\pmb s^{+’}=0. $$
通过Charnes-Cooper转换,得到线性规划模型: $$ \begin{aligned} \min &~~\rho=t-\frac1m\sum_{i=1}^m\frac{S_i^-}{x_{i0}}\\ s.t. &~~ 1=t+\frac1{q_1+q_2}\left(\sum_{r=1}^{q_1}\frac{S_r^+}{y_{r0}}+\sum_{r=1}^{q_2}\frac{S_r^{+’}}{y_{r0}}\right)\\ &~~ tx_{i0}=\sum_{j=1}^nx_{ij}\Lambda_j + S_i^- ~(i=1,2,\dots,m)\\ &~~ ty_{r0}=\sum_{j=1}^n y_{rj}\Lambda_j-S_r^+ ~(r=1,2,\dots,q_1)\\ &~~ tz_{r0}=\sum_{j=1}^n z_{rj}\Lambda_j-S_r^+ ~(r=1,2,\dots,q_2)\\ &~~ \Lambda_j\ge0,S_i^-\ge0, S_r^+\ge0,t\ge0 \end{aligned} $$ 由线性规划的可行解$\left(\rho^*,\vec\Lambda^*,t^*,\pmb S^{-*}, \pmb S^{+*}, \pmb S^{+’*}\right)$,可以解出原始模型的可行解$\left(\rho^*,\vec\lambda^*,\pmb s^{-*}, \pmb s^{+*}, \pmb s^{+’*}\right)$,
$$ \pmbλ^* = \frac{\pmbΛ^*}{t^*},~\pmb s^{-*}=\frac{\pmb S^{-*}}{t^*} ,~\pmb s^{+*}=\frac{\pmb S^{+*}}{t^*} ,~\pmb s^{+’*}=\frac{\pmb S^{+’*}}{t^*} $$
若$\rho^*=1$,则称该$DMU$为SBM-efficient,此时$\pmb s^{-*}=0, \pmb s^{+*}=0, \pmb s^{+’*}=0$;
若$\rho^*<1$,则称该$DMU$为SBM-inefficient,对于一个SBM-inefficient的决策单元(假设为$DMU_k$),其投入和产出满足:
$$ \displaylines{ \vec x_k = X\vec\lambda^* + \pmb s^{-*}\\ \vec y_k = Y\vec\lambda^* - \pmb s^{+*}\\ \vec z_k = Z\vec\lambda^* + \pmb s^{+’*} } $$
由于得到了投入过量和产出不足的具体数值,因此我们可以对该可比决策单元进行优化,称为SBM投射(SBM-projection): $$ \displaylines{ \vec x_k \leftarrow \vec x_k - \pmb s^{-*}\\ \vec y_k \leftarrow \vec y_k + \pmb s^{+*}\\ \vec z_k \leftarrow \vec z_k - \pmb s^{+’*} } $$
Python代码实现
为了便于编程,我们将以上规划问题写成矩阵形式, $$ \begin{aligned} \min &~~ \rho=C\cdot \pmb X\\ s.t. &~~ A\cdot\pmb X = b\\ &~~ \pmb X\ge0 \end{aligned} $$ 其中自变量为 $$ \pmb X=\left[ {\color{red} \lambda_1,\lambda_2,\dots,\lambda_n,}~~t,~~ {\color{blue} S_1^-,S_2^-,\dots,S_m^-,}~~ {\color{green} S_1^+,S_2^+,\dots,S_{q_1}^+,~~ S_1^{+’},S_2^{+’},\dots,S_{q_2}^{+’}} \right]^\rm T, $$ 目标函数系数矩阵为 $$ C=\left[ {\color{red} 0,0,\dots,0,}~~1,~~{\color{blue} -\frac{1}{mx_{10}},-\frac{1}{mx_{20}},\dots,-\frac{1}{mx_{m0}}},~~{\color{green}0,\dots,0} \right], $$ 约束条件方程系数为 $$ \displaylines{ A=\left[ \begin{matrix} \color{red} 0 & \color{red}\cdots & \color{red}0 & 1 & \color{blue}0 & \color{blue}\cdots & \color{blue}0 & \color{green}\alpha_{1} & \color{green}\cdots & \color{green}\alpha_{q_1} & \color{green}\beta_{1} & \color{green}\dots & \color{green}\beta_{q_2}\\ \\ \\ \color{red}x_{11} & \color{red}\cdots & \color{red}x_{1n} & -x_{10} & \color{blue}1 & \color{blue}\cdots & \color{blue}0 & \color{green}0 & \color{green}\cdots & \color{green}0 & \color{green}0 & \color{green}\cdots & \color{green}0\\ & \color{red}\vdots &&&& \color{blue}\ddots &&& \color{green}\vdots &&& \color{green}\vdots\\ \color{red}x_{m1} & \color{red}\cdots & \color{red}x_{mn} & -x_{m0} & \color{blue}0 & \color{blue}\cdots & \color{blue}1 & \color{green}0 & \color{green}\cdots & \color{green}0 & \color{green}0 & \color{green}\cdots & \color{green}0\\ \\ \\ \color{red}y_{11} & \color{red}\cdots & \color{red}y_{1n} & -y_{10} & \color{blue}0 & \color{blue}\cdots & \color{blue}0 & \color{green}-1 & \color{green}\cdots & \color{green}0 & \color{green}0 & \color{green}\cdots & \color{green}0\\ & \color{red}\vdots &&&& \color{blue}\vdots &&& \color{green}\ddots &&& \color{green}\vdots\\ \color{red}y_{q_11} & \color{red}\cdots & \color{red}y_{q_1n} & -y_{q_10} & \color{blue}0 & \color{blue}\cdots & \color{blue}0 & \color{green}0 & \color{green}\cdots & \color{green}-1 & \color{green}0 & \color{green}\cdots & \color{green}0\\ \\ \\ \color{red}z_{11} & \color{red}\cdots & \color{red}z_{1n} & -z_{10} & \color{blue}0 & \color{blue}\cdots & \color{blue}0 & \color{green}0 & \color{green}\cdots & \color{green}0 & \color{green}1 & \color{green}\cdots & \color{green}0\\ & \color{red}\vdots &&&& \color{blue}\vdots &&& \color{green}\vdots &&& \color{green}\ddots\\ \color{red}z_{q_21} & \color{red}\cdots & \color{red}z_{q_2n} & -z_{q_20} & \color{blue}0 & \color{blue}\cdots & \color{blue}0 & \color{green}0 & \color{green}\cdots & \color{green}0 & \color{green}0 & \color{green}\cdots & \color{green}1\\ \end{matrix} \right],\\ \alpha_{r} = \frac{1}{\left(q_1+q_2\right)y_{r0}}~\left( r=1,2,\dots,q_1\right),\\ \beta_{r} = \frac{1}{\left(q_1+q_2\right)z_{r0}}~\left( r=1,2,\dots,q_2\right), } $$
约束条件常数项为 $$ b=\left[ 1,~~0,0,\dots,0 \right]^\rm T $$
代码结构来自wonder1322的博客
|
|
补充:求解对偶模型的过程
线性规划的矩阵形式
学习SBM模型的时候遇到了对偶规划这一步骤,之前没有接触过,在B站上找了一个教程对照着推导了一遍。
原始的线性规划模型,自变量是$\vec \mu=[\mu_1, \mu_2, \dots,\mu_q],\vec\nu=[\nu_1,\nu_2,\dots,\nu_m]$。
注意:虽然规划模型中有$X$、$Y$,但是这是代表可比决策单元的投入量和产出量的,是已知的数据,所以并不是变量。 $$ \begin{aligned} \max &~~ z=\sum_{r=1}^q\mu_{r}Y_{rk}\\ s.t. &~~ \sum_{r=1}^q\mu_{r}Y_{rj}-\sum_{i=1}^m\nu_{i}X_{ij}\le0~(\mu_r\ge0, \nu_i\ge0)\\ &~~ \sum_{i=1}^m\nu_iX_{ik}=1\\ &~~ i=1,2,\dots,m;~r=1,2,\dots,q;~j=1,2,\dots,n \end{aligned} $$ 先转换为矩阵形式,自变量向量记为$\pmb X$, $$ \begin{aligned} \max &~~ Z=C\cdot \pmb X\\ s.t. &~~ A\cdot\pmb X\le b\\ &~~ \pmb X\ge0 \end{aligned} $$ 其中由于等式$\sum_{i=1}^m\nu_iX_{ik}=1$,导致自变量的自由度减1,这里剔除$\nu_m$,即 $$ \pmb X=\left[\mu_1, \mu_2, \dots,\mu_q,\nu_1,\nu_2,\dots,\nu_{m-1}\right]^\rm T. $$ 目标函数的系数向量为 $$ C=\left[ Y_{1k}, Y_{2k}, \dots,Y_{qk},0,0,\dots,0 \right], $$ 其中有$m-1$个$0$。
除了要满足$\pmb X\ge0$以外,还应保证$\nu_m\ge0$,即 $$ \nu_m=\frac{1-\sum_{i=1}^{m-1}\nu_iX_{ik}}{X_{mk}}\ge0 \Leftrightarrow \sum_{i=1}^{m-1}\nu_iX_{ik}\le1. $$ 对于模型中的主要约束条件,消去$\nu_m$后得到 $$ \sum_{r=1}^q\mu_{r}Y_{rj}+ \sum_{i=1}^{m-1}\nu_{i}\left(\frac{X_{ik}X_{mj}}{X_{mk}} -X_{ij}\right)\le \frac{X_{mj}}{X_{mk}}, j=1,2,\dots,n. $$ 以上两式整合得到$A\cdot\pmb X\le b$,则
$$ \displaylines{ A_{(n+1)\times (q+m-1)}= \left[ \begin{matrix} Y_{11} & Y_{21} & \cdots & Y_{q1} & \alpha_{11} & \alpha_{21} & \cdots & \alpha_{m-1,1}\\ Y_{12} & Y_{22} & \cdots & Y_{q2} & \alpha_{12} & \alpha_{22} & \cdots & \alpha_{m-1,2}\\ &&\vdots&&&&\vdots\\ Y_{1n} & Y_{2n} & \cdots & Y_{qn} & \alpha_{1n} & \alpha_{2n} & \cdots & \alpha_{m-1,n}\\ 0 & 0 & \cdots & 0 & X_{1k} & X_{2k} & \cdots & X_{m-1,k} \end{matrix} \right],\\ {\rm where}~\alpha_{ij} = \left(\frac{X_{ik}X_{mj}}{X_{mk}} -X_{ij}\right),b=\left[ \frac{X_{m1}}{X_{mk}}, \frac{X_{m2}}{X_{mk}}, \dots, \frac{X_{mn}}{X_{mk}},1 \right]^\rm T } $$
至此得到矩阵形式的全部系数。
线性规划的对偶形式
这里补充一下关于线性规划问题转换为其对偶问题的数学推导4。已知有如下线性规划 $$ \begin{aligned} {\pmb P:~~}\max &~~ Z=C\cdot \pmb X\\ s.t. &~~ A\cdot\pmb X\le b\\ &~~ \pmb X\ge0 \end{aligned} $$ 的对偶形式为 $$ \begin{aligned} {\pmb D:~~}\min &~~ W={\pmb Y}^{\rm T}\cdot b\\ s.t. &~~ A^{\rm T}\cdot {\pmb Y}\ge C^{\rm T}\\ &~~ \pmb Y\ge0 \end{aligned} $$ $\pmb D$问题的自变量为$\pmb Y=[\lambda_1,\lambda_2,\dots,\lambda_{n+1}]^\rm T$,目标函数展开后为 $$ W={\pmb Y}^{\rm T}\cdot b=\sum_{j=1}^n\frac{X_{mj}}{X_{mk}}\lambda_j+\lambda_{n+1}. $$ 主要约束条件展开后为 $$ \begin{aligned} & \sum_{j=1}^n\lambda_j Y_{rj}\ge Y_{rk}\\ & \sum_{j=1}^n \lambda_j \left( \frac{X_{ik}X_{mj}}{X_{mk}}-X_{ij} \right)\ge0 \\ &r=1,2,\dots,q;~i=1,2,\dots,m \end{aligned} $$ 将目标函数代入第二个不等式,得到 $$ \sum_{j=1}^n\lambda_jX_{ij}\le X_{ik}\left(\lambda_{n+1}+W\right). $$ 以上对偶规划模型的多项式形式如下所示: $$ \begin{aligned} \min &~~ W=\sum_{j=1}^n\frac{X_{mj}}{X_{mk}}\lambda_j+\lambda_{n+1} \\ s.t. &~~ \sum_{j=1}^n\lambda_j Y_{rj}\ge Y_{rk}~(\lambda_j\ge0)\\ &~~ \sum_{j=1}^n\lambda_jX_{ij}\le X_{ik}\left(\lambda_{n+1}+W\right)\\ &~~ i=1,2,\dots,m;~r=1,2,\dots,q;~j=1,2,\dots,n \end{aligned} $$
-
李成宇. 中国工业绿色发展质量测度及影响因素研究[D]. 山东科技大学, 2020. DOI: 10.27275/d.cnki.gsdku.2020.000319. ↩︎
-
Tone, K. (2001). A slacks-based measure of efficiency in data envelopment analysis. European Journal of Operational Research, 130(3), 498-509. DOI: 10.1016/S0377-2217(01)00324-1 ↩︎