环境数据分析课程的大作业，主要目的应用一下课上学到的一些数据分析方法。

通过爬虫获取我国沿海海水水质的监测数据；
以散点图直观反映水质类别的分布和随时间变化情况；
将化学需氧量数据转换为正态分布，以海区/省份为分类变量进行单因素方差分析；
将无机氮数据转换为正态分布，用Pearson分析和线性回归分析考察化学需氧量和无机氮数据的相关性；
利用机器学习，从多个污染指标数据预测海区分类。

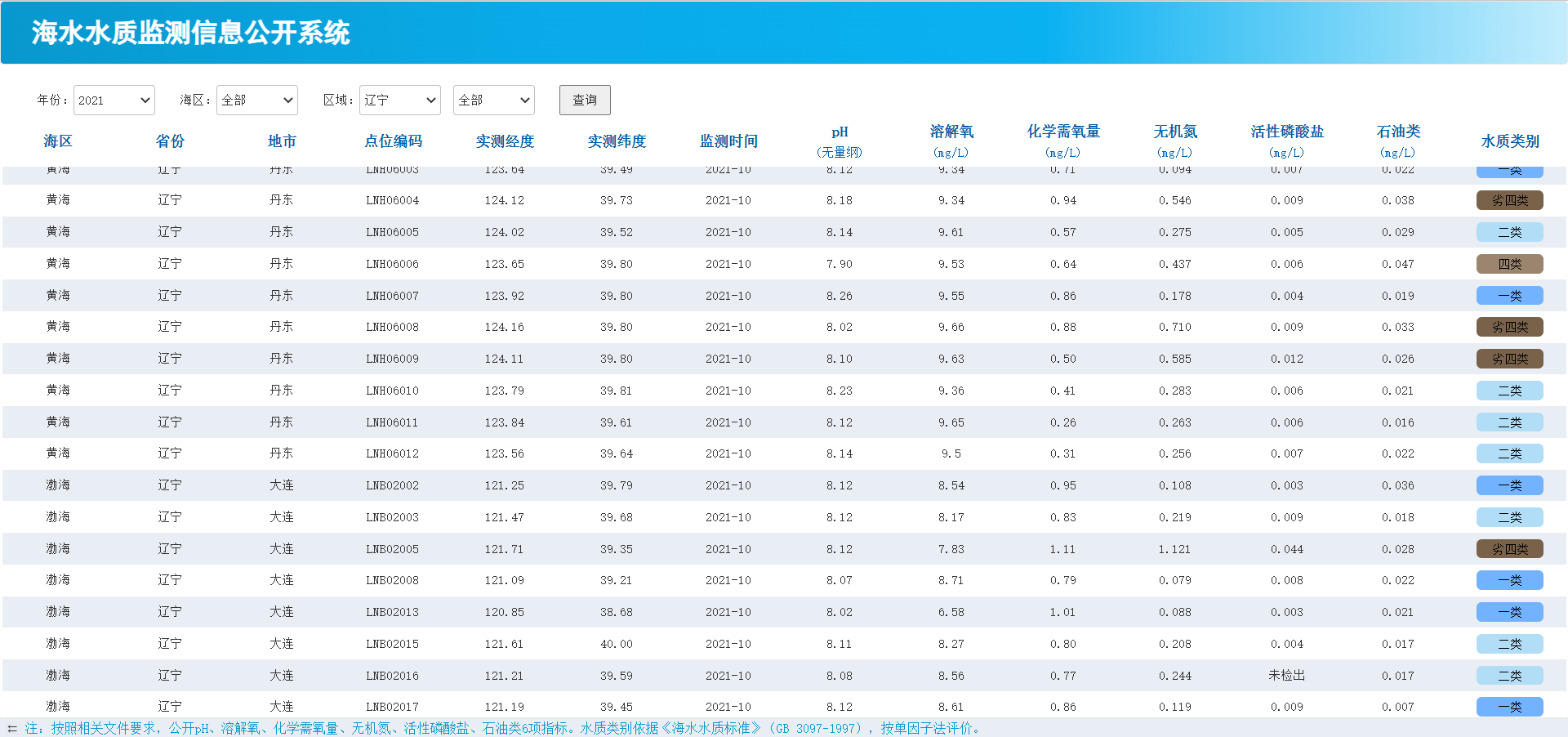
数据获取

爬虫

来源：生态环境部的海水水质监测信息公开系统。网址：http://ep.nmemc.org.cn:8888/Water/

1
2
3
4
5


from selenium import webdriver
import pandas as pd

wd = webdriver.Chrome()
wd.get('http://ep.nmemc.org.cn:8888/Water/')

对动态网页的表格设置过滤属性。这里先筛选获取2020年的数据。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


year = wd.find_element_by_id('ddl_year')
sea = wd.find_element_by_id('ddl_sea')
province = wd.find_element_by_id('ddl_province')
city = wd.find_element_by_id('ddl_city')

year.send_keys('2020')
sea.send_keys('全部')
province.send_keys('全部')
city.send_keys('全部')

botton = wd.find_element_by_id('btn')
botton.click()

获取表头和数据，并整理成二维数组的类型。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


header = wd.find_element_by_id('gridHd')
heads = header.text.replace('\n','').split(' ')
body = wd.find_element_by_id('gridDatas')
predatas = body.text.split('\n')

total = int(len(predatas)/2)
data = []
for i in range(total):
    row = predatas[2*i].split(' ')
    row.append(predatas[2*i+1])
    data.append(row)

把2021年的数据也添加到数组里，转换成data frame。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


year.send_keys('2021')
botton.click()

body = wd.find_element_by_id('gridDatas')
predatas = body.text.split('\n')

total = int(len(predatas)/2)
for i in range(total):
    row = predatas[2*i].split(' ')
    row.append(predatas[2*i+1])
    data.append(row)
df = pd.DataFrame(data, columns=heads)

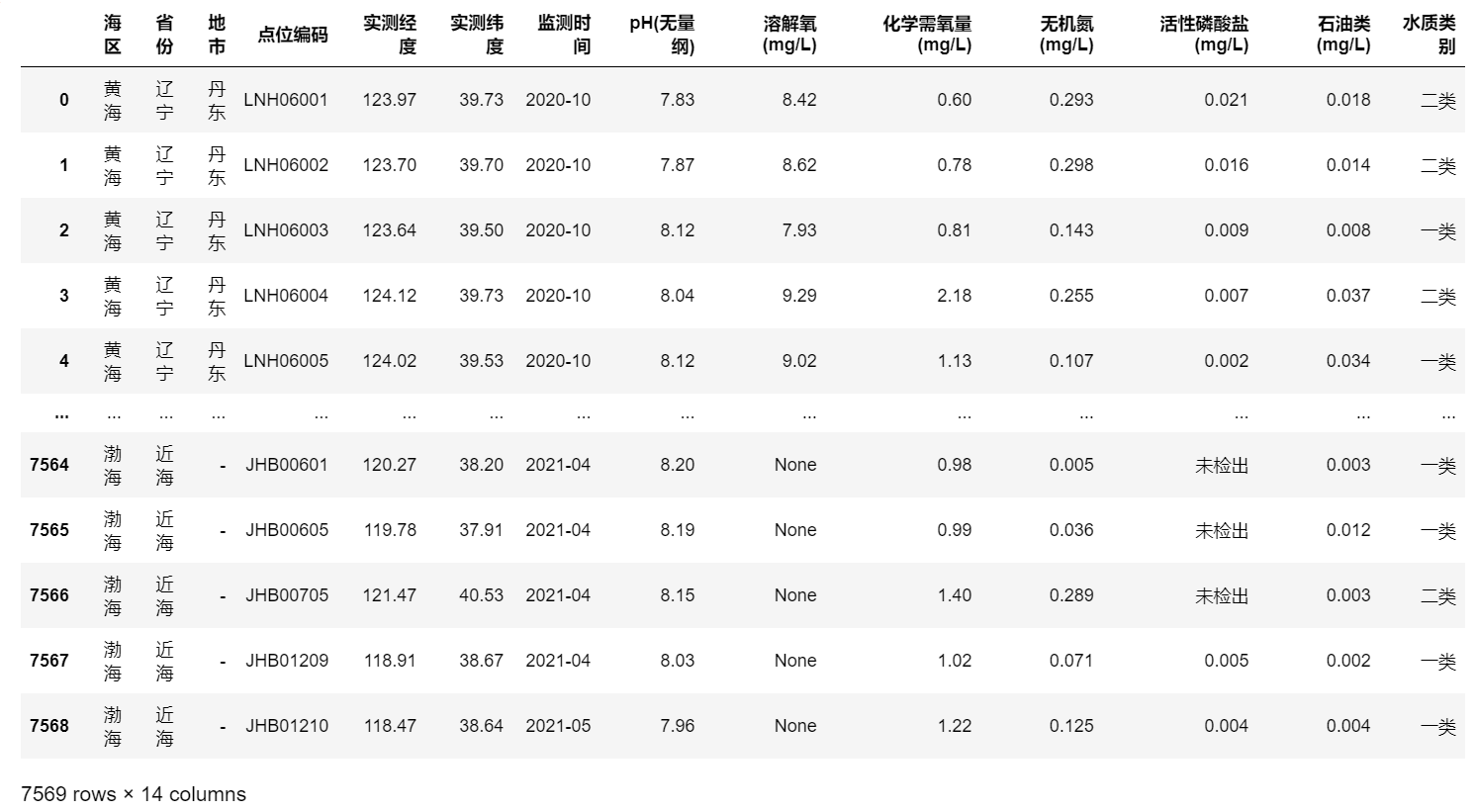
数据整理和保存

发现部分监测点数据位移，原因是部分监测点的溶解氧数据缺失，还有一些数据点的溶解氧和石油类数据都缺失。对这些监测点的信息进行修正，缺失的地方用None标记。

1
2
3
4
5
6
7
8
9


for i in range(len(df)):
    if df['水质类别'][i]==None:
        for j in range(13,8,-1):
            df.iloc[i,j] = df.iloc[i,j-1]
        df.iloc[i,8] = None
for i in range(len(df)):
    if df['水质类别'][i]==None:
        df.iloc[i,13] = df.iloc[i,12]
        df.iloc[i,12] = None

保存数据到本地。此时数据全都以字符串保存。缺失值标记为“None”，低于检出限的数据标记为“未检出”，或根据检出限的值标记为“<0.01”或“<0.1”。

1
2


wd.quit()
df.to_pickle('./Data.pkl')

水质类别动态变化

根据每个月水质监测数据的经纬度信息和水质类别作图。

1
2
3
4
5


import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator

data = pd.read_pickle('./Data.pkl')

查看一下水质类别有哪些分类，执行data['水质类别'].value_counts()，输出：

1
2
3
4
5
6


一类     4082
二类     1343
劣四类    1154
三类      514
四类      476
Name: 水质类别, dtype: int64

将经纬度数据转换成浮点型。

1
2


data['实测经度'] = pd.to_numeric(data['实测经度'])
data['实测纬度'] = pd.to_numeric(data['实测纬度'])

定义返回某年某月所有监测点坐标的函数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


def getlongitude(dataframe,year,month):
    longitude_by_level = []
    a = dataframe[(dataframe['监测时间']==year+'-'+month)&(dataframe['水质类别']=='一类')]['实测经度']
    b = dataframe[(dataframe['监测时间']==year+'-'+month)&(dataframe['水质类别']=='二类')]['实测经度']
    c = dataframe[(dataframe['监测时间']==year+'-'+month)&(dataframe['水质类别']=='三类')]['实测经度']
    d = dataframe[(dataframe['监测时间']==year+'-'+month)&(dataframe['水质类别']=='四类')]['实测经度']
    e = dataframe[(dataframe['监测时间']==year+'-'+month)&(dataframe['水质类别']=='劣四类')]['实测经度']
    longitude_by_level.append(a)
    longitude_by_level.append(b)
    longitude_by_level.append(c)
    longitude_by_level.append(d)
    longitude_by_level.append(e)
    return longitude_by_level

def getlatitude(dataframe,year,month):
    latitude_by_level = []
    a = dataframe[(dataframe['监测时间']==year+'-'+month)&(dataframe['水质类别']=='一类')]['实测纬度']
    b = dataframe[(dataframe['监测时间']==year+'-'+month)&(dataframe['水质类别']=='二类')]['实测纬度']
    c = dataframe[(dataframe['监测时间']==year+'-'+month)&(dataframe['水质类别']=='三类')]['实测纬度']
    d = dataframe[(dataframe['监测时间']==year+'-'+month)&(dataframe['水质类别']=='四类')]['实测纬度']
    e = dataframe[(dataframe['监测时间']==year+'-'+month)&(dataframe['水质类别']=='劣四类')]['实测纬度']
    latitude_by_level.append(a)
    latitude_by_level.append(b)
    latitude_by_level.append(c)
    latitude_by_level.append(d)
    latitude_by_level.append(e)
    return latitude_by_level

定义画出某年某月水质类别分布图的函数。将网上找的我国海岸线轮廓作为底图（网上下载下来是shp格式的，但是找到了一个很好的网站，可以将shp图层文件转换成位图 https://mapshaper.org/）。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


def draw_plot(year,month,longitude_by_level,latitude_by_level):
    fig, ax = plt.subplots(figsize=((128-106),(42-14)))

    ax.scatter(longitude_by_level[0], latitude_by_level[0], c='paleturquoise', s=100, EdgeColor='k')
    ax.scatter(longitude_by_level[1], latitude_by_level[1], c='c', s=100, EdgeColor='k')
    ax.scatter(longitude_by_level[2], latitude_by_level[2], c='cadetblue', s=100, EdgeColor='k')
    ax.scatter(longitude_by_level[3], latitude_by_level[3], c='teal', s=100, EdgeColor='k')
    ax.scatter(longitude_by_level[4], latitude_by_level[4], c='darkslategrey', s=100, EdgeColor='k')

    plt.rcParams['font.sans-serif']=['SimHei']###解决中文乱码
    plt.rcParams['axes.unicode_minus']=False

    ax.legend(['一类','二类','三类','四类','劣四类'],fontsize=30,loc='upper left')

    ax.axis([106,128,14,42])
    major_locator=MultipleLocator(5)
    ax.xaxis.set_major_locator(major_locator)
    ax.grid()
    plt.xticks(fontsize=30)
    plt.yticks(fontsize=30)
    plt.xlabel('经度(E°)',fontsize=30)
    plt.ylabel('纬度(N°)',fontsize=30)
    plt.title(str(year)+'年'+str(month)+'月我国沿海监测点水质类别情况',fontsize=40)

    img = plt.imread("land-sea.jpg")
    zoom = 0.0221
    height,width = len(img)*zoom,len(img[0])*zoom
    x,y = 121.0,22.1
    ax.imshow(img,extent=[x-width/2,x+width/2,y-height/2,y+height/2])

    plt.savefig('../沿海检测点水质类别变化/'+year+'-'+month+'.jpg', dpi=200)

生成2020-2021年每月的水质分布图。

1
2
3
4
5
6


for year in ['2020','2021']:
    for month in ['01','02','03','04','05','06','07','08','09','10','11','12']:
        print('Drawing '+year+'-'+month)
        longitude_by_level = getlongitude(data,year,month)
        latitude_by_level = getlatitude(data,year,month)
        draw_plot(year,month,longitude_by_level,latitude_by_level)

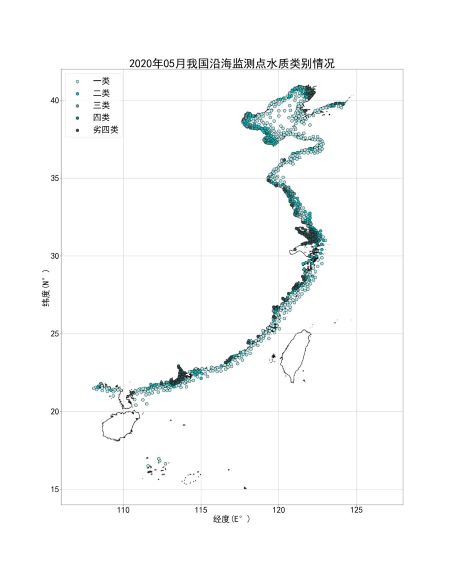
将图片拼接成GIF动图。

1
2
3
4
5
6


import imageio, os, sys
jpg_lst = os.listdir('../沿海检测点水质类别变化/')
frames = []
for img in jpg_lst:
    frames.append(imageio.imread('../沿海检测点水质类别变化/' + img))
imageio.mimsave("../沿海检测点水质类别变化/result.gif", frames, 'GIF', duration=0.5)

result

简单数据分析：正态性检验、方差分析、Pearson分析和线性回归

以“化学需氧量(mg/L)”为研究数据，考察不同海区/省份之间的海水COD差异性。首先将数据转换为数值类型，标记为“未检出”的数据记为0。由于方差分析适用于正态分布的样本，因此先对数据进行分布检验，变换为接近正态分布的形式后再进行方差分析。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
import numpy as np
import random
import seaborn as sns
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
from sklearn.linear_model import LinearRegression
plt.rcParams['font.sans-serif']=['SimHei']###解决中文乱码
plt.rcParams['axes.unicode_minus']=False

数据清理和转换

首先读取数据，转换成浮点型。

1
2
3
4
5


data = pd.read_pickle('./Data.pkl')
for i in cod.index:
    if cod[i] == '未检出':
        cod[i] = '0'
cod = pd.to_numeric(cod)

从原始数据的直方图大致看一下分布情况。

1
2
3
4
5


fig, ax = plt.subplots(figsize=(15,5))
sns.histplot(cod, bins=150)
plt.xlim(min(cod), max(cod))
plt.xlabel('COD(mg/L)')
plt.ylabel('Frequency')

可以看出样本是明显有偏的，计算样本的偏度（Skewness）和峰度（Kurtosis）。

1
2
3


s = cod.skew()
k = cod.kurt()
print('偏度 = '+str(s)+', 峰度 = '+str(k))

`1`	`偏度 = 4.58614227400281, 峰度 = 43.47585104239013`

偏度$S>0$，表明样本正偏，数据出现右侧长尾；峰度$K>6$，表明分布陡峭。尝试通过取对数得到接近正态的分布。这里考虑到0的数据比较多，若采用$x’=\lg(x+10^{-n})$的转换方法，会在$x=-n$的地方出现一个异常峰，所以决定舍弃0数据。

1
2
3
4
5
6


cod2 = pd.Series.copy(cod,deep=True)
for i in cod2.index:
    if cod[i] == 0:
        del cod2[i]
    else:
        cod2[i] = np.log10(cod[i])

1
2
3
4
5


fig, ax = plt.subplots(figsize=(7,5))
sns.histplot(cod2, bins=100)
plt.xlim(min(cod2), max(cod2))
plt.xlabel('log10(COD)')
plt.ylabel('Frequency')

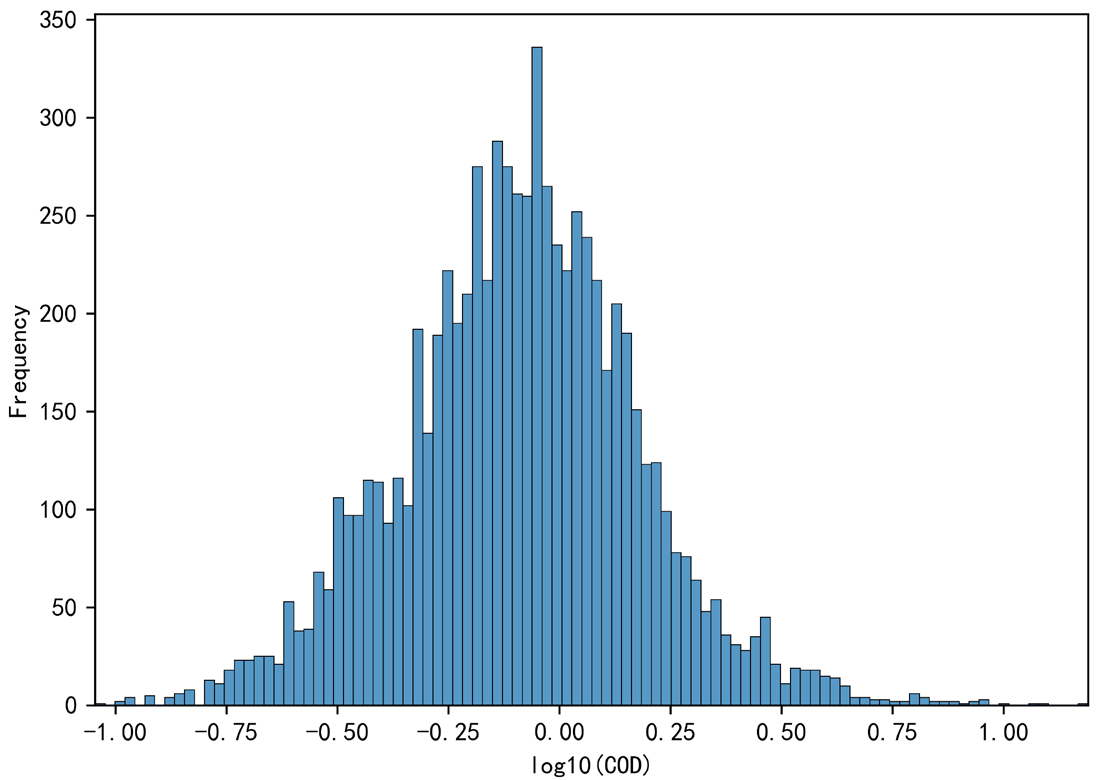
1
2
3


s = cod2.skew()
k = cod2.kurt()
print('偏度 = '+str(s)+', 峰度 = '+str(k))

`1`	`偏度 = 0.08821022006460341, 峰度 = 0.6118708597667646`

转换后的样本偏度约等于零，可以近似认为样本是无偏的。考虑到样本量>7500，根据大数定理认为样本总体符合正态分布。

事实上如果用K-S检验，还是会发现不能通过正态性检验的。可能是因为数据的差异性大，所以样本数量还远远不够；也有可能是因为数据本身的采样有偏，事实上水质监测数据确实不是完全随机时刻和取点的，会受到采样点设置偏好的影响。这里只是凭借大数定理和Q-Q图，定性地认为服从正态分布。

用Q-Q图辅助判断，处理后的数据点更好地分布在对角线上。

1
2
3
4
5


fig, ax = plt.subplots(1,2,figsize=(12,5))
stats.probplot(cod, dist="norm", plot=ax[0])
stats.probplot(cod2, dist="norm", plot=ax[1])
ax[0].set_title('Original Data')
ax[1].set_title('Logarithmic Data')

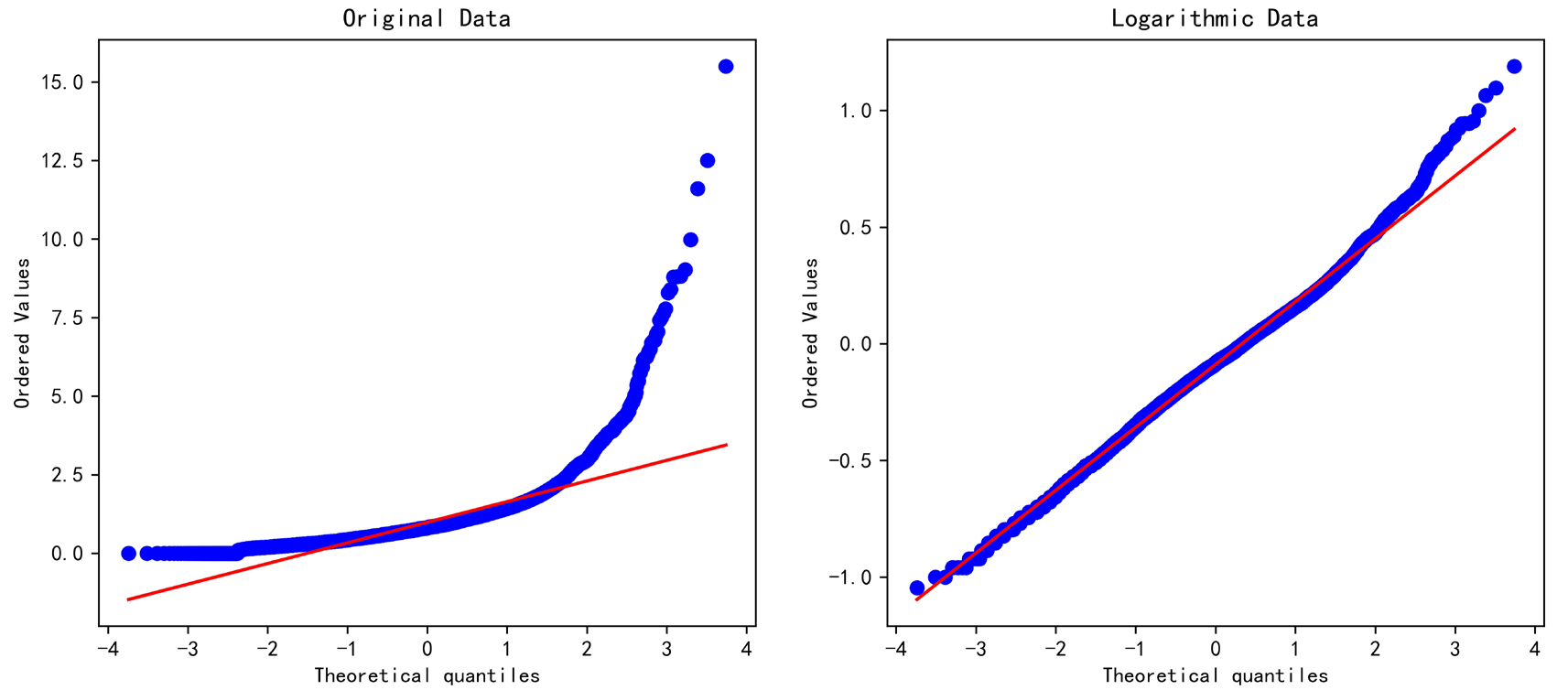
方差分析

获取海区和省份的数据（定类数据），和对数化的COD一起合成data frame。

1
2
3
4
5


anova_data = pd.DataFrame(columns=['海区','省份','logCOD'])
for i in cod2.index:
    sea = data['海区'][i]
    province = data['省份'][i]
    anova_data.loc[i] = [sea, province, cod2[i]]

先用箱型图看一下四大海区的分布差异。

1
2


fig, ax = plt.subplots(figsize=(7,5))
sns.boxplot(x='海区',y='logCOD',data = anova_data)

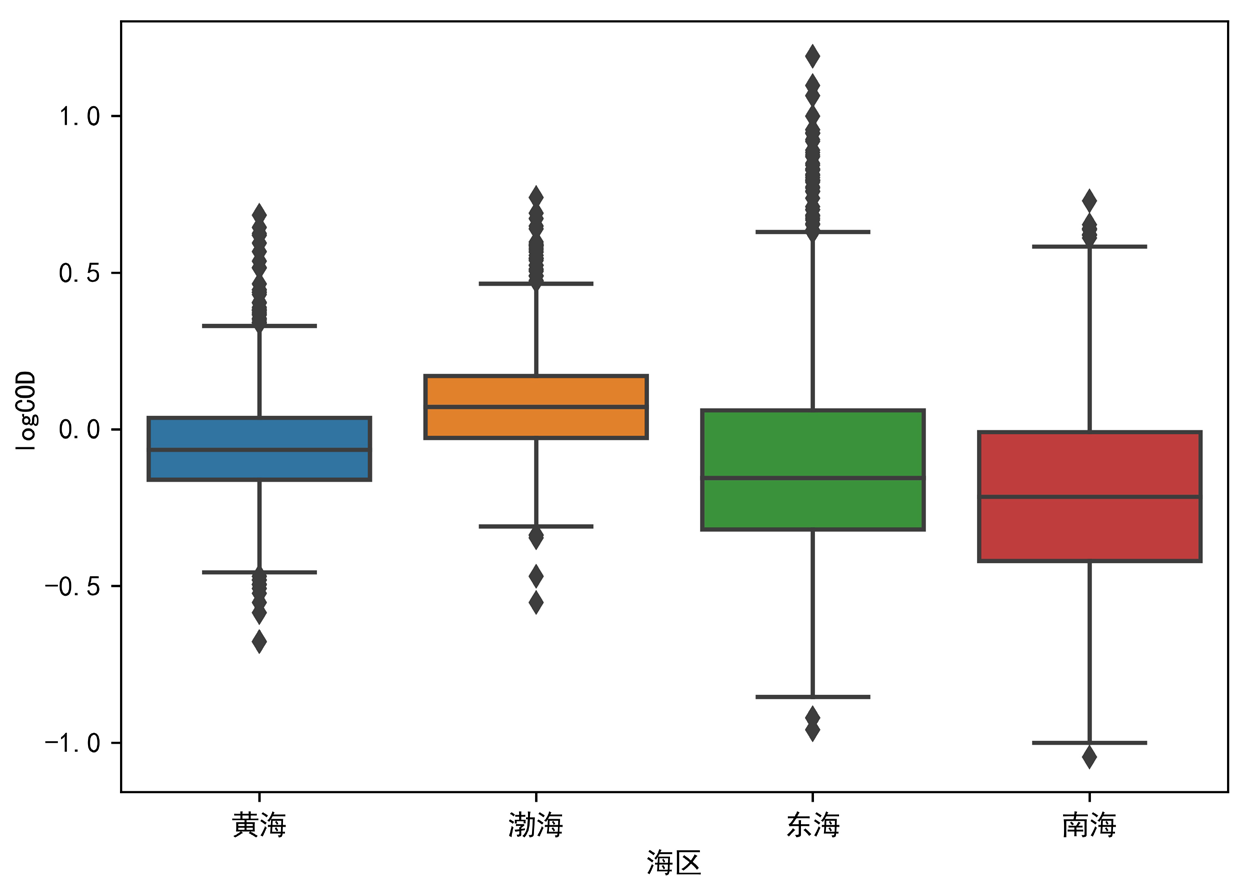
单因素方差分析。

1
2
3


model = ols('logCOD ~ 海区',data=anova_data).fit()
anova_table = anova_lm(model, typ = 2)
print(anova_table)

1
2
3


              sum_sq      df           F         PR(>F)
海区         73.816704     3.0  390.048152  1.941560e-235
Residual  473.062501  7499.0         NaN            NaN

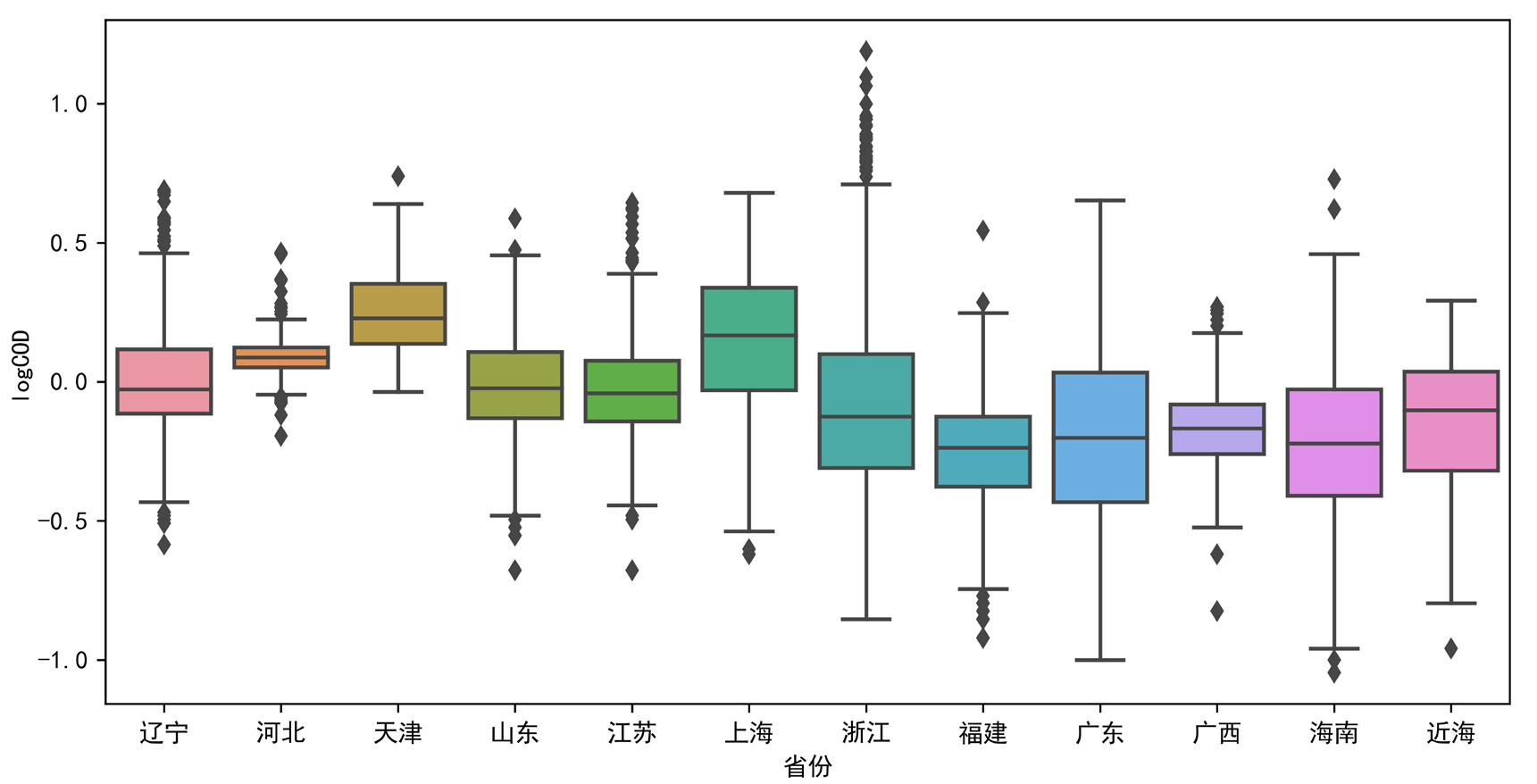
省份分布差异同理。

1
2


fig, ax = plt.subplots(figsize=(10,5))
sns.boxplot(x='省份',y='logCOD',data = anova_data)

1
2
3


model = ols('logCOD ~ 省份',data=anova_data).fit()
anova_table = anova_lm(model, typ = 2)
print(anova_table)

1
2
3


              sum_sq      df           F  PR(>F)
省份        102.311302    11.0  156.722959     0.0
Residual  444.567902  7491.0         NaN     NaN

单因素方差分析P值均低于0.01，表明海区和省份因素都会使得COD数据产生显著差异。

Pearson相关分析

上面的分析是针对COD（定序变量）和海区/省份（定类变量）之间关系的分析。接下来选取“无机氮(mg/L)”数据，与COD数据进行定序变量的相关性分析。由于Pearson相关性分析要求两个变量均服从正态分布，因此对无机氮数据也要先进行数据清理和转换，取以10为底的对数。Q-Q图依然可以反映出处理前后的正态性变化。

1
2
3
4
5


ni = data['无机氮(mg/L)']
ni = pd.to_numeric(ni)
ni2 = ni.copy(deep=True)
for i in ni.index:
    ni2[i] = np.log10(np.sqrt(ni[i]))

1
2
3
4
5


fig, ax = plt.subplots(1,2,figsize=(12,5))
stats.probplot(ni, dist="norm", plot=ax[0])
stats.probplot(ni2, dist="norm", plot=ax[1])
ax[0].set_title('Original Data')
ax[1].set_title('Logarithmic Data')

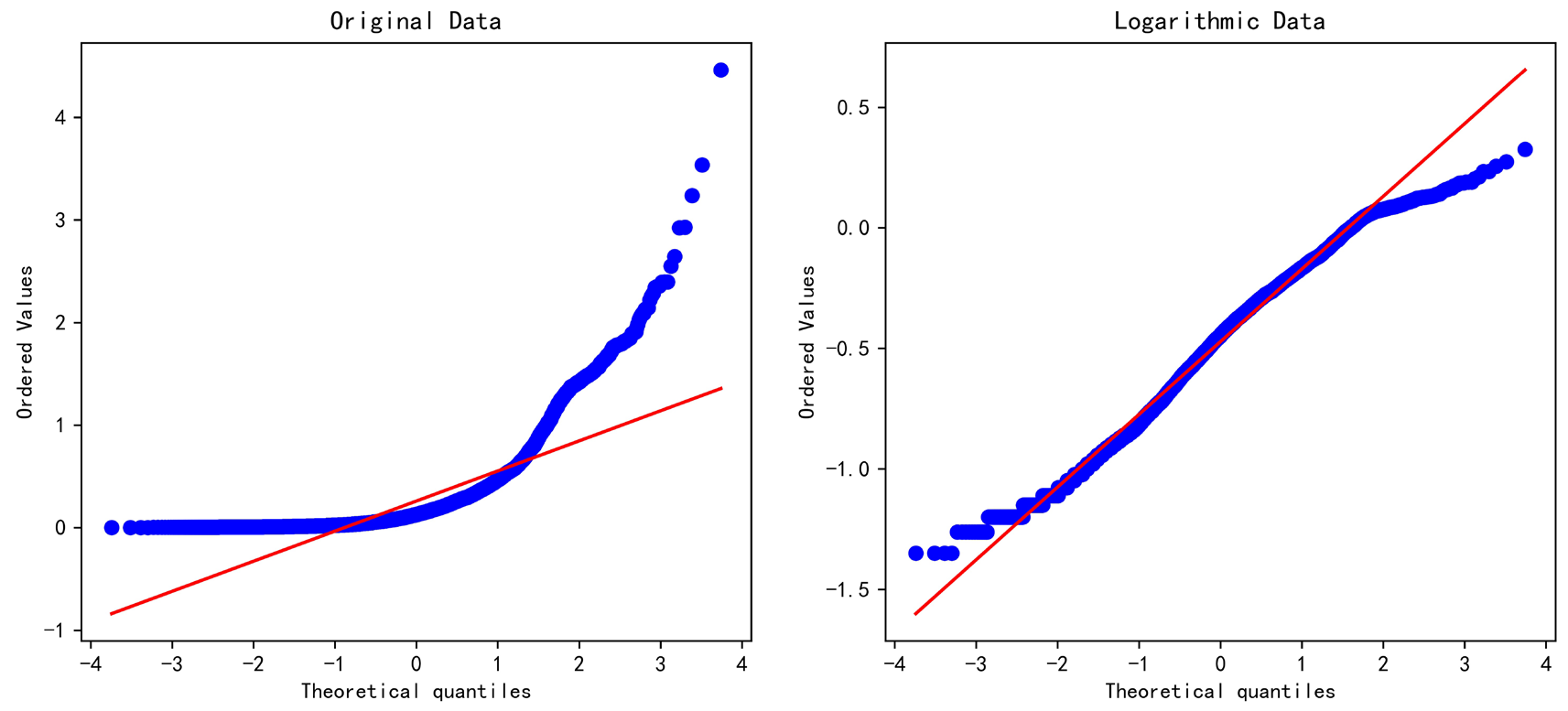
由于有些监测点只有化学需氧量数据，没有无机氮数据，因此需要进行数据清理，将这些监测点删除。

1
2
3


for i in range(len(data)):
    if i not in cod2.index:
        del ni2[i]

进行Pearson检验。

1
2


r,p = stats.pearsonr(ni2,cod2)
print('Pearson检验，相关系数 = %f, P值 = %f'%(r,p))

`1`	`Pearson检验，相关系数 = 0.446809, P值 = 0.000000`

$r\in(0.4,0.6)$，认为$\lg(\rm COD)$和$\lg(\rm N)$之间为中等程度正相关。通过散点图分布情况也可以感性判断出这一规律。

线性回归

1
2
3
4
5
6
7


model = LinearRegression()
model.fit(ni.values.reshape((-1, 1)),
          cod.values)
predict_y = model.predict(ni2.values.reshape((-1, 1)))
print('线性回归斜率：',model.coef_,
      '\n截距：',model.intercept_,
      '\nR方：',model.score(ni.values.reshape((-1, 1)),cod.values))

1
2
3


线性回归斜率： [1.10361078] 
截距： 0.7039567080504857 
R方： 0.24820547860780384

1
2
3
4
5


fig, ax = plt.subplots(figsize=(5,5))
plt.scatter(ni2,cod2,s=1)
plt.plot(ni2,predict_y,c='k')
plt.xlabel('logN')
plt.ylabel('logCOD')

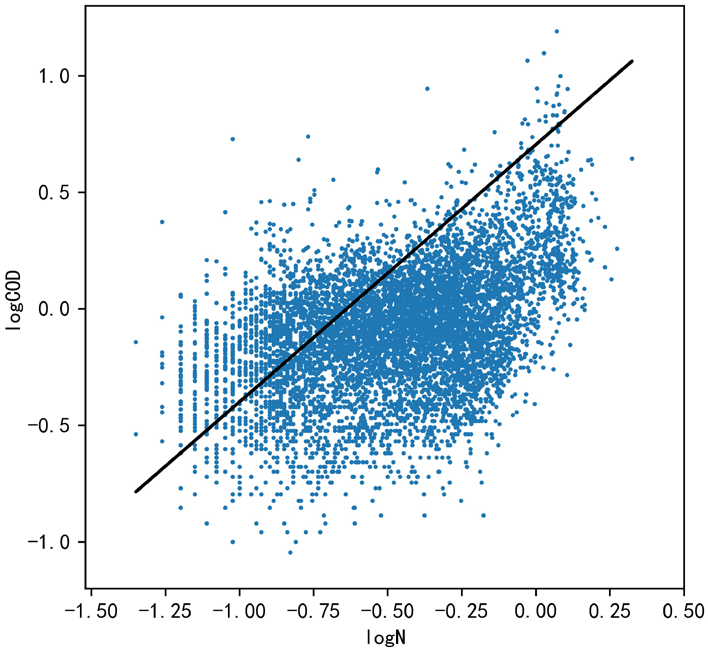
考虑到海水地理位置对相关性的影响，再分海区绘制散点图和回归曲线。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


sl_data = pd.DataFrame(columns=['海区','logN','logCOD'])
for i in cod2.index:
    sea = data['海区'][i]
    sl_data.loc[i] = [sea, ni2[i], cod2[i]]

seas = ['黄海','渤海','东海','南海']
predicts = []
for i in range(4):
    model = LinearRegression()
    model.fit(sl_data[sl_data['海区']==seas[i]]['logN'].values.reshape((-1, 1)),
              sl_data[sl_data['海区']==seas[i]]['logCOD'].values)
    predict_y = model.predict(sl_data[sl_data['海区']==seas[i]]['logN'].values.reshape((-1, 1)))
    predicts.append(predict_y)
    print(seas[i],
          '\n线性回归斜率：',model.coef_,
          '\n截距：',model.intercept_,
          '\nR方：',model.score(sl_data[sl_data['海区']==seas[i]]['logN'].values.reshape((-1, 1)),
                               sl_data[sl_data['海区']==seas[i]]['logCOD'].values) )

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


黄海 
线性回归斜率： [0.26539399] 
截距： 0.081372330354296 
R方： 0.14307643170710227
渤海 
线性回归斜率： [0.27080498] 
截距： 0.20731753294507865 
R方： 0.1352474744941149
东海 
线性回归斜率： [0.63405663] 
截距： 0.0898058817788494 
R方： 0.3550328969220925
南海 
线性回归斜率： [0.36912331] 
截距： 0.012211050912901922 
R方： 0.1838150602146984

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41


fig, ax = plt.subplots(2,2,figsize=(10,10))

ax[0,0].scatter(sl_data[sl_data['海区']=='黄海']['logN'],
                sl_data[sl_data['海区']=='黄海']['logCOD'],
                s=3, c='g')
ax[0,0].plot(sl_data[sl_data['海区']=='黄海']['logN'], predicts[0], c='k')
ax[0,0].set_title('黄 海')
ax[0,0].set_xlabel('logN')
ax[0,0].set_ylabel('logCOD')
ax[0,0].set_xlim(-1.52, 0.5)
ax[0,0].set_ylim(-1.2,1.3)

ax[0,1].scatter(sl_data[sl_data['海区']=='渤海']['logN'],
                sl_data[sl_data['海区']=='渤海']['logCOD'],
                s=3, c='y')
ax[0,1].plot(sl_data[sl_data['海区']=='渤海']['logN'], predicts[1], c='k')
ax[0,1].set_title('渤 海')
ax[0,1].set_xlabel('logN')
ax[0,1].set_ylabel('logCOD')
ax[0,1].set_xlim(-1.52, 0.5)
ax[0,1].set_ylim(-1.2,1.3)

ax[1,0].scatter(sl_data[sl_data['海区']=='东海']['logN'],
                sl_data[sl_data['海区']=='东海']['logCOD'],
                s=3, c='purple')
ax[1,0].plot(sl_data[sl_data['海区']=='东海']['logN'], predicts[2], c='k')
ax[1,0].set_title('东 海')
ax[1,0].set_xlabel('logN')
ax[1,0].set_ylabel('logCOD')
ax[1,0].set_xlim(-1.52, 0.5)
ax[1,0].set_ylim(-1.2,1.3)

ax[1,1].scatter(sl_data[sl_data['海区']=='南海']['logN'],
                sl_data[sl_data['海区']=='南海']['logCOD'],
                s=3, c='brown')
ax[1,1].plot(sl_data[sl_data['海区']=='南海']['logN'], predicts[3], c='k')
ax[1,1].set_title('南 海')
ax[1,1].set_xlabel('logN')
ax[1,1].set_ylabel('logCOD')
ax[1,1].set_xlim(-1.52, 0.5)
ax[1,1].set_ylim(-1.2,1.3)

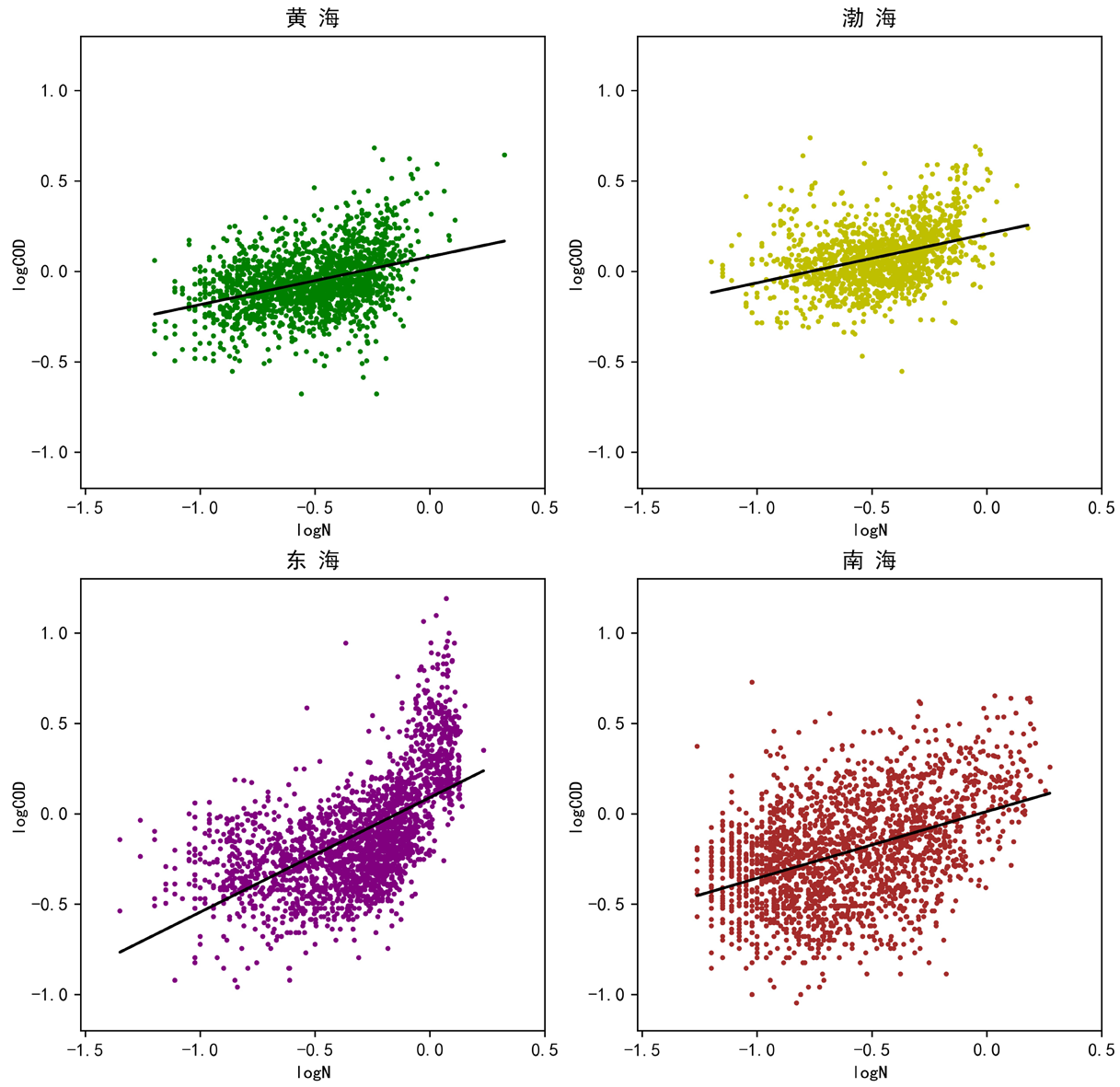
机器学习

为了从多个污染指标的层面上对不同海区的差异进行分析，以“化学需氧量(mg/L)”、“无机氮(mg/L)”、“活性磷酸盐(mg/L)”、“石油类(mg/L)”这四个指标作为自变量，将“海区”作为因变量，尝试用5种不同的模型进行机器学习，并找出预测准确度最高的模型进行进一步分析。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

plt.rcParams['font.sans-serif']=['SimHei']###解决中文乱码
plt.rcParams['axes.unicode_minus']=False

from sklearn import model_selection
from sklearn.preprocessing import StandardScaler

from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier

from sklearn.model_selection import cross_val_score
from sklearn.metrics import classification_report, confusion_matrix, f1_score, roc_curve, roc_auc_score, precision_score, accuracy_score, recall_score, explained_variance_score, mean_absolute_error, mean_squared_error, r2_score 

数据清理

首先把数据转换为数值类型。将标记为“未检出”、“<0.01”、“<0.1”的数据转换为0。将因变量（海区）数值化，标记成0~3。

海区	数值化
黄海	0
渤海	1
东海	2
南海	3

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


for i in range(len(data)):
    if data['海区'][i]=='黄海':
        data['海区'][i] = 0
    elif data['海区'][i]=='渤海':
        data['海区'][i] = 1
    elif data['海区'][i]=='东海':
        data['海区'][i] = 2
    else:
        data['海区'][i] = 3
    
    for item in ['化学需氧量(mg/L)','无机氮(mg/L)','活性磷酸盐(mg/L)','石油类(mg/L)']:
        if type(data[item][i])==str and (data[item][i] == '未检出' or data[item][i][0] == '<'):
            data[item][i] = '0'
D = data.loc[:,['海区','化学需氧量(mg/L)','无机氮(mg/L)','活性磷酸盐(mg/L)','石油类(mg/L)']]
for item in D.columns:
    D[item] = pd.to_numeric(D[item])

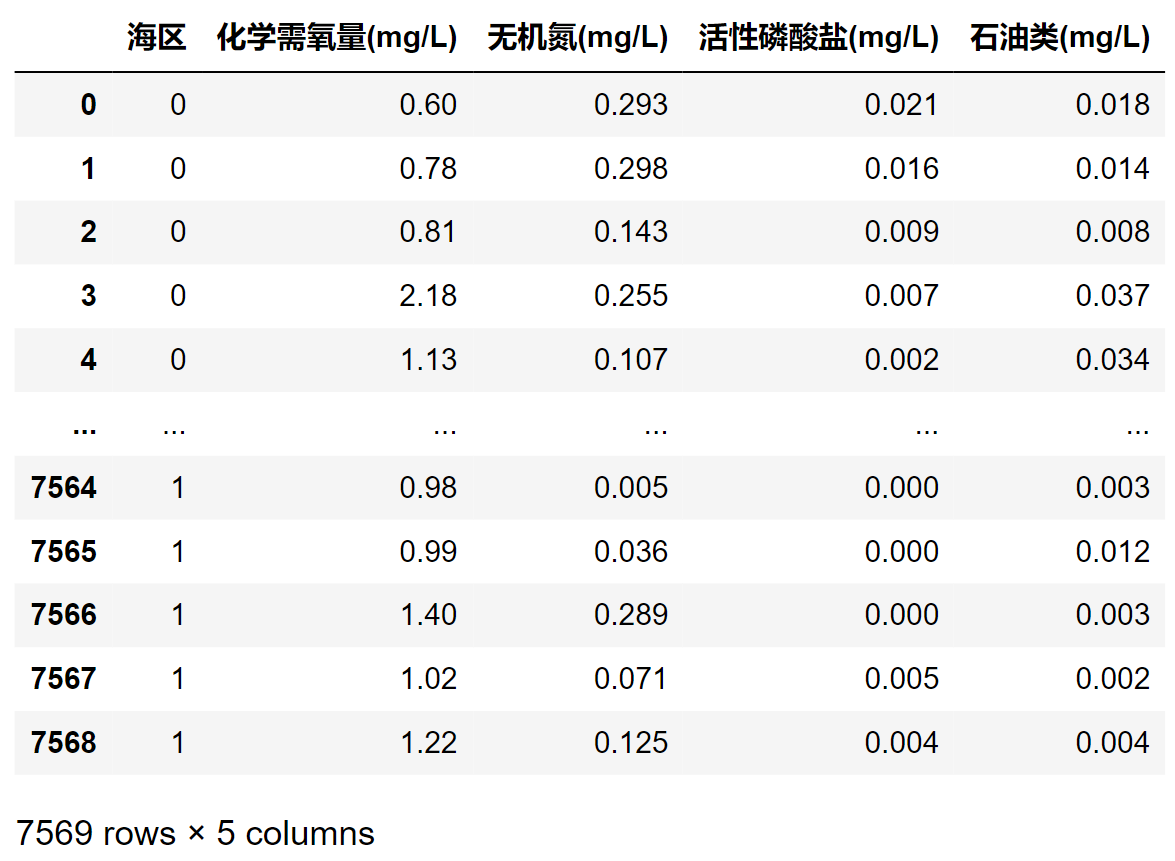
其中任何一项数据缺失的监测点都删除，最后把清理后的因变量保存为一维数组Y，自变量保存为四维数组X。

1
2
3
4
5
6


nanlist = []
for i in range(len(D.values)):
    if True in np.isnan(D.values[i]):
        nanlist.append(i)
X = np.delete(D.iloc[:,1:5].values, nanlist, axis=0)
Y = np.delete(D.iloc[:,0].values, nanlist, axis=0)

多模型比较

划分训练集和测试机，特征缩放。

1
2
3
4


x_train,x_test, y_train,y_test = model_selection.train_test_split(X, Y, test_size=0.2, random_state=1)
sc = StandardScaler()
x_train = sc.fit_transform(x_train)
x_test = sc.transform(x_test)

用于对比的5种模型分别是：Decision Tree决策树、K-Nearest Neighbors K-最近邻（KNN）、Logistic Regression 逻辑回归、SVM支持向量机 (SVM)、Random Forest Tree随机森林。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


# 1. Decision Tree 决策树
tree_model = DecisionTreeClassifier(max_depth = 10, criterion = 'entropy')
tree_model.fit(x_train, y_train)
tree_yhat = tree_model.predict(x_test)

# 2. K-Nearest Neighbors K-最近邻 (KNN)
n = 20
knn = KNeighborsClassifier(n_neighbors = n)
knn.fit(x_train, y_train)
knn_yhat = knn.predict(x_test)

# 3. Logistic Regression 逻辑回归
lr = LogisticRegression()
lr.fit(x_train, y_train)
lr_yhat = lr.predict(x_test)

# 4. SVM  支持向量机 (SVM)
svm = SVC(probability=True) #SVM要制作ROC曲线，必须probability=True，默认值False
svm.fit(x_train, y_train)
svm_yhat = svm.predict(x_test)

# 5. Random Forest Tree 随机森林
rf = RandomForestClassifier(max_depth = 10)
rf.fit(x_train, y_train)
rf_yhat = rf.predict(x_test)

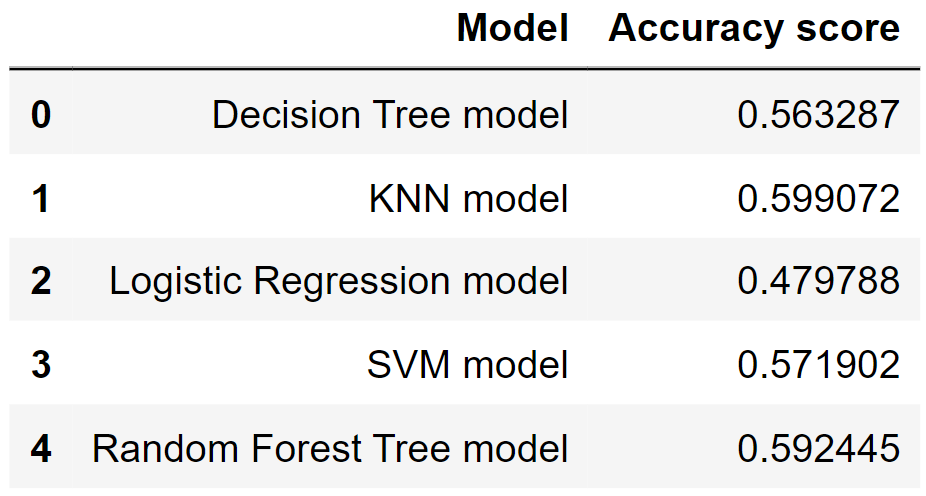
分别用accuracy score和F1-score来衡量不同模型的效果。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


pd.DataFrame({
    'Model':         ['Decision Tree model',
                      'KNN model',
                      'Logistic Regression model',
                      'SVM model',
                      'Random Forest Tree model'],
    'Accuracy score':[accuracy_score(y_test, tree_yhat),
                      accuracy_score(y_test, knn_yhat),
                      accuracy_score(y_test, lr_yhat),
                      accuracy_score(y_test, svm_yhat),
                      accuracy_score(y_test, rf_yhat)]
    })

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


pd.DataFrame({
    'Model':              ['Decision Tree model',
                           'KNN model',
                           'Logistic Regression model',
                           'SVM model',
                           'Random Forest Tree model'],
    '黄海(0)':[f1_score(y_test, tree_yhat, average=None)[0],
                 f1_score(y_test, knn_yhat, average=None)[0],
                 f1_score(y_test, lr_yhat, average=None)[0],
                 f1_score(y_test, svm_yhat,average=None)[0],
                 f1_score(y_test, rf_yhat, average=None)[0]],
    '渤海(1)':   [f1_score(y_test, tree_yhat, average=None)[1],
                 f1_score(y_test, knn_yhat, average=None)[1],
                 f1_score(y_test, lr_yhat, average=None)[1],
                 f1_score(y_test, svm_yhat,average=None)[1],
                 f1_score(y_test, rf_yhat, average=None)[1]],
    '东海(2)':[f1_score(y_test, tree_yhat, average=None)[2],
                 f1_score(y_test, knn_yhat, average=None)[2],
                 f1_score(y_test, lr_yhat, average=None)[2],
                 f1_score(y_test, svm_yhat,average=None)[2],
                 f1_score(y_test, rf_yhat, average=None)[2]],
    '南海(3)':   [f1_score(y_test, tree_yhat, average=None)[3],
                 f1_score(y_test, knn_yhat, average=None)[3],
                 f1_score(y_test, lr_yhat, average=None)[3],
                 f1_score(y_test, svm_yhat,average=None)[3],
                 f1_score(y_test, rf_yhat, average=None)[3]],
    })

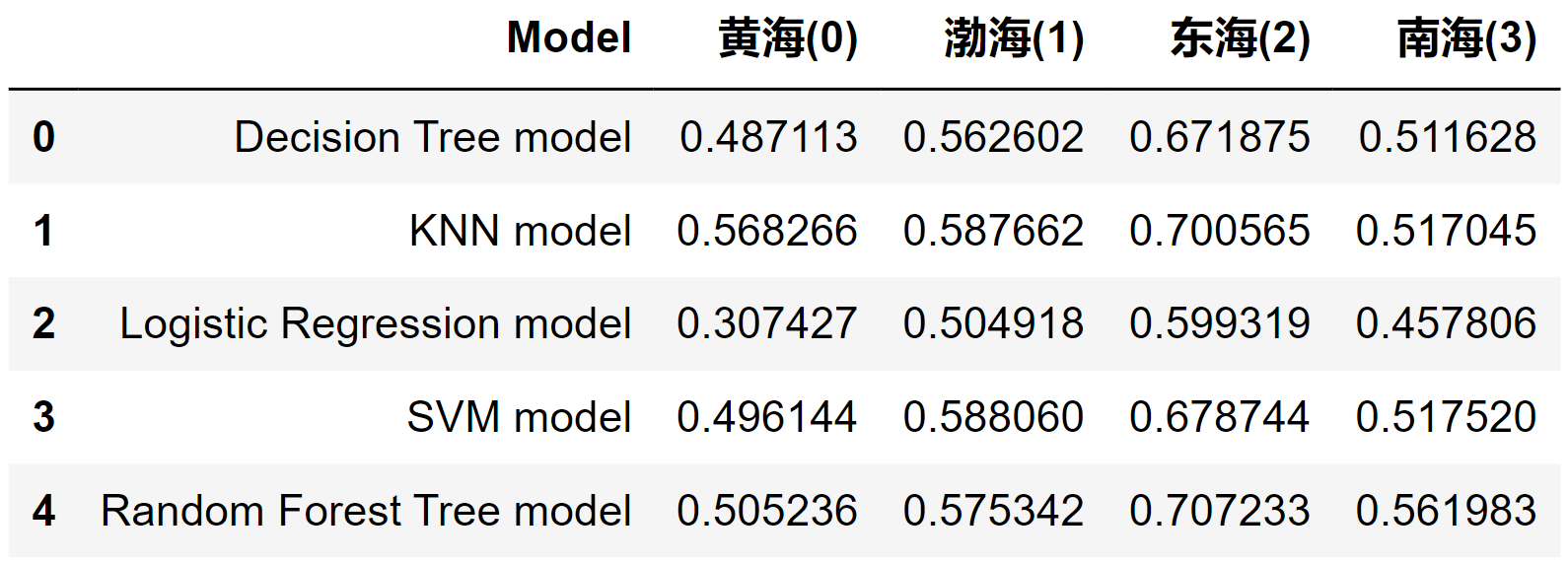
通过混淆矩阵也可以判断不同模型的预测能力，并且比较不同海区的数据被正确判断或误判为其他海区的可能性。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


tree_matrix = confusion_matrix(y_test, tree_yhat, labels = [0, 1, 2, 3]) # Decision Tree
knn_matrix = confusion_matrix(y_test, knn_yhat, labels = [0, 1, 2, 3]) # K-Nearest Neighbors
lr_matrix = confusion_matrix(y_test, lr_yhat, labels = [0, 1, 2, 3]) # Logistic Regression
svm_matrix = confusion_matrix(y_test, svm_yhat, labels = [0, 1, 2, 3]) # Support Vector Machine
rf_matrix = confusion_matrix(y_test, rf_yhat, labels = [0, 1, 2, 3]) # Random Forest Tree

def plot_confusion_matrix(ax, cm, classes, title):    
    plot = ax.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
    ax.set_title(title)
    ax.set_xticks([0,1,2,3])
    ax.set_xticklabels(classes)
    ax.set_yticks([0,1,2,3])
    ax.set_yticklabels(classes)
    ax.set_ylabel('真实海区')
    ax.set_xlabel('预测海区')
    return plot

classes = ['黄海(0)','渤海(1)','东海(2)','南海(3)']
fig, ax = plt.subplots(2,3,figsize=(16,8))
a = plot_confusion_matrix(ax[0][0], tree_matrix, classes=classes, title='Decision Tree')
b = plot_confusion_matrix(ax[0][1], knn_matrix, classes=classes, title='KNN')
c = plot_confusion_matrix(ax[0][2], lr_matrix, classes=classes, title='Logistic Regression')
d = plot_confusion_matrix(ax[1][0], svm_matrix, classes=classes, title='SVM')
e = plot_confusion_matrix(ax[1][1], rf_matrix, classes=classes, title='Random Forest Tree')
fig.colorbar(a, ax = ax[0][0])
fig.colorbar(b, ax = ax[0][1])
fig.colorbar(c, ax = ax[0][2])
fig.colorbar(d, ax = ax[1][0])
fig.colorbar(e, ax = ax[1][1])
fig.delaxes(ax[1][2])
plt.tight_layout()
plt.show()

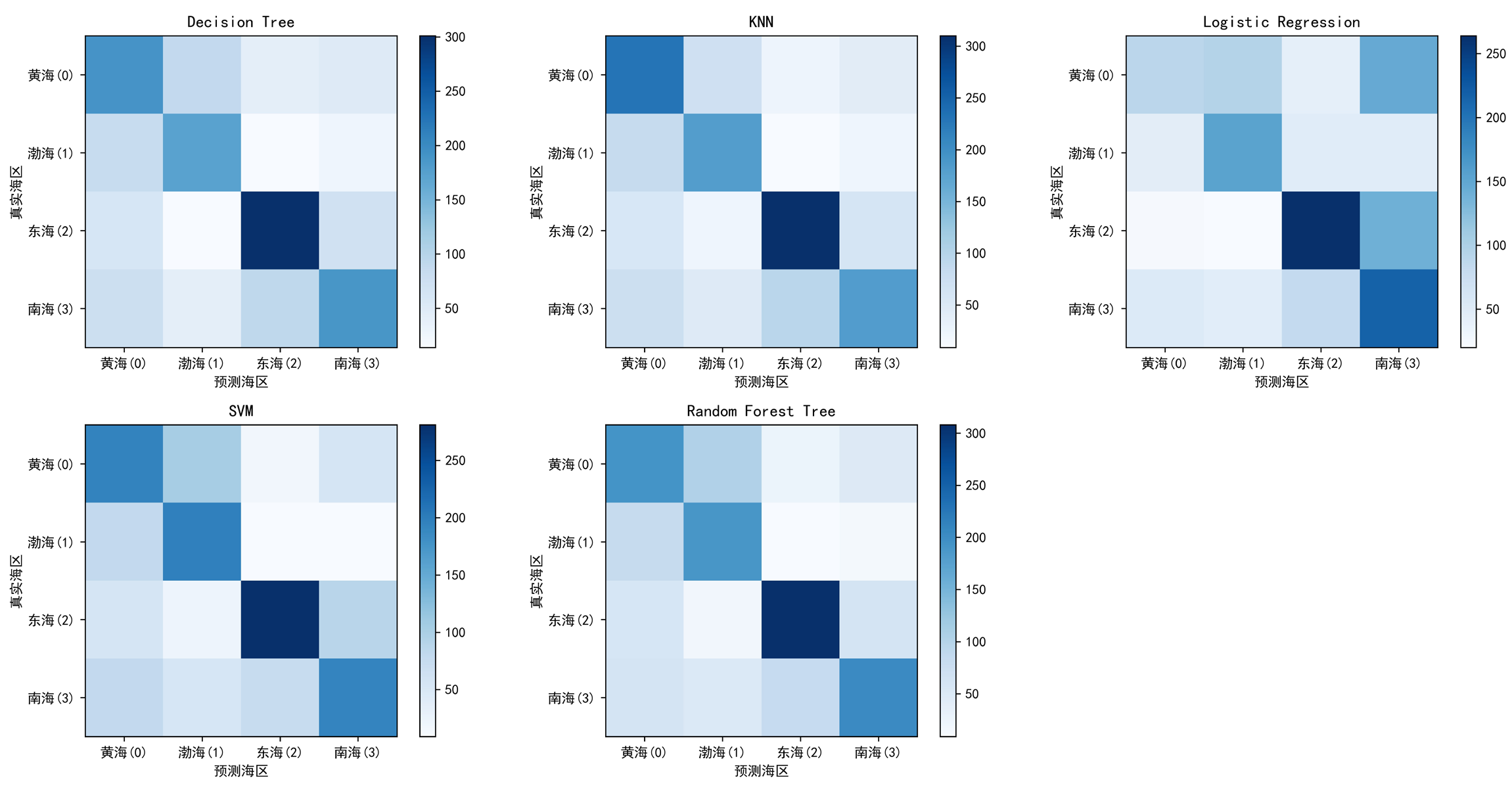
KNN模型

综合以上，认为在当前的参数设置下KNN模型具有最好的解释力。输出KNN模型的分类报告。

1

print(classification_report(y_test, knn_yhat))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


              precision    recall  f1-score   support

           0       0.52      0.62      0.57       370
           1       0.56      0.61      0.59       295
           2       0.71      0.70      0.70       446
           3       0.59      0.46      0.52       398

    accuracy                           0.60      1509
   macro avg       0.60      0.60      0.59      1509
weighted avg       0.60      0.60      0.60      1509

本模型采用的是多分类模型，但是传统的ROC曲线和AUC只能用于描述不同于“0-1”分类模型。首先需要将因变量的测试集转换成类似于0-1分类的多维矩阵。

1
2


y_test0 = np.array([[ 1 if y_test[i]==j else 0 for j in range(4) ] for i in range(len(y_test))], dtype=float)
y_test0

1
2
3
4
5
6
7


array([[0., 0., 1., 0.],
       [0., 0., 1., 0.],
       [0., 1., 0., 0.],
       ...,
       [1., 0., 0., 0.],
       [0., 1., 0., 0.],
       [0., 0., 1., 0.]])

将转换后的因变量测试集和自变量测试集都按行展开，例如

1

y_test0.ravel()

`1`	`array([0., 0., 1., ..., 0., 1., 0.])`

采用macro方法对多分类数据进行处理，然后再计算ROC曲线和AUC值。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


y_pred=knn.predict_proba(x_test)[:,:]

roc_score = roc_auc_score(y_test, y_pred, multi_class='ovo', average='macro')
y_test0 = np.array([[ 1 if y_test[i]==j else 0 for j in range(4) ] for i in range(len(y_test))], dtype=float)

fpr,tpr, thresholds = roc_curve(y_test0.ravel(), y_pred.ravel(), pos_label=True)

fig, ax = plt.subplots(1,1,figsize=(8,6))
ax.plot(fpr,tpr,"r",linewidth = 3)
ax.set_title("多分类ROC曲线")
ax.plot([0, 1], [0, 1], 'k--')
ax.grid()
ax.set_xlabel("假正率")
ax.set_ylabel("真正率")
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.text(0.15,0.9,"AUC = "+str(round(roc_score,4)))
plt.show()

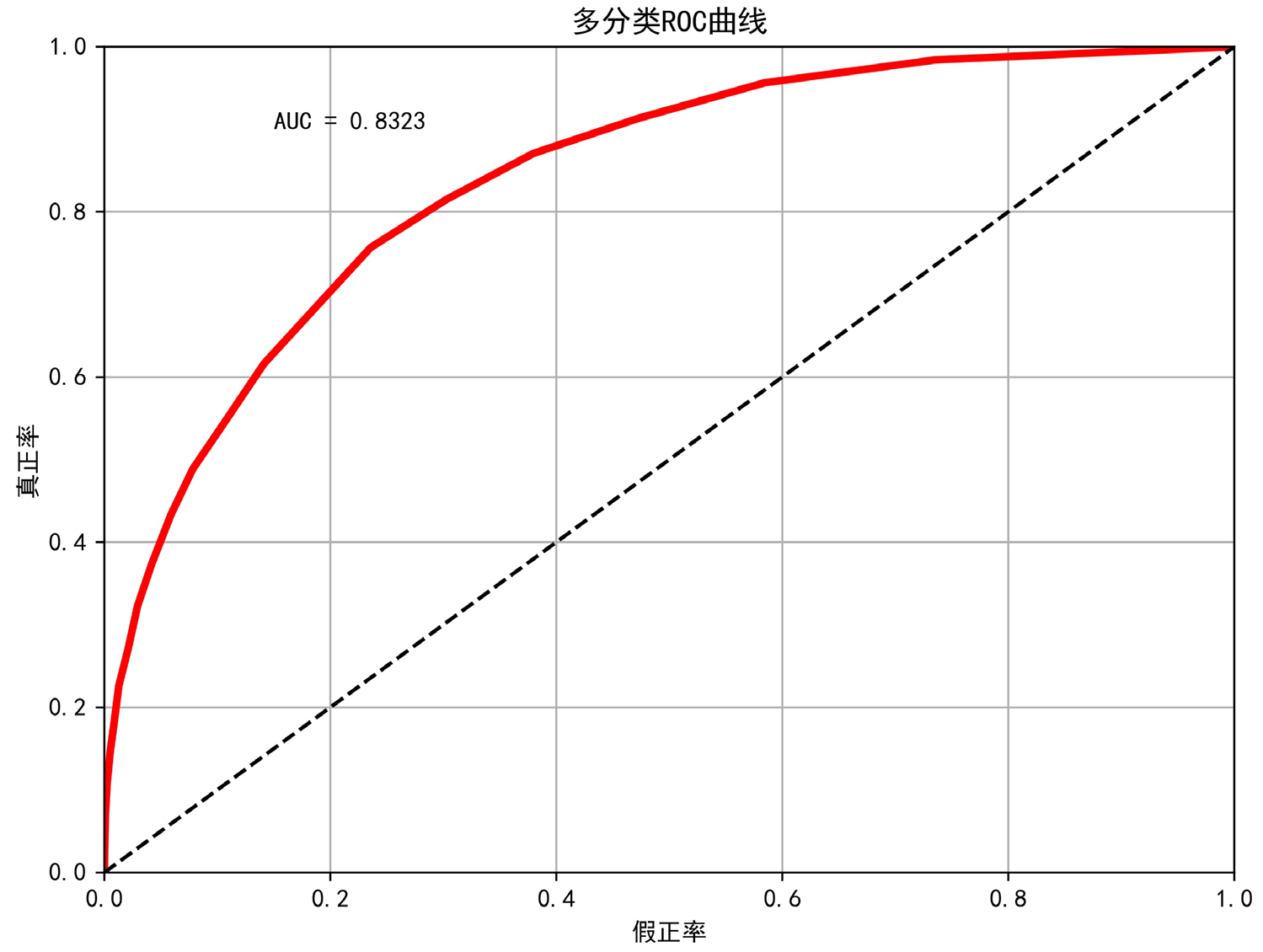
限制本模型预测能力的可能原因有：分类精细度和依据不合适；没有找到最关键的自变量；数据采集有偏；模型训练迭代次数不足。

数据获取#

爬虫#

数据整理和保存#

水质类别动态变化#

简单数据分析：正态性检验、方差分析、Pearson分析和线性回归#

数据清理和转换#

方差分析#

Pearson相关分析#

线性回归#

机器学习#

数据清理#

多模型比较#

KNN模型#