Barrel distortion(桶形畸变)是一种成像画面呈桶形膨胀的畸变现象,通常在广角镜头下出现。最近在调试生态监测相机时就遇到了非常典型的桶形畸变,会影响到对于监测对象的定位精确性。
网上找到对Barrel distortion的描述如下。
Barrel distortion: When straight lines are curved inwards in a shape of a barrel, this type of aberration is called “barrel distortion”. Commonly seen on wide angle lenses, barrel distortion happens because the field of view of the lens is much wider than the size of the image sensor and hence it needs to be “squeezed” to fit. As a result, straight lines are visibly curved inwards, especially towards the extreme edges of the frame.1

为了便于理解Barrel distortion并尝试自行解决问题,我构建了一个极其简化的理想模型:
将相机理想化为一个点,其到实物平面的垂足为$O(0,0)$,距离为$h$。平面上某一点相对于$O$的坐标为$P_1(x_1, y_1)$,该点对应的相机视野张角为$\theta_1$。则 $$ \tan{\frac{\theta_1}{2}}=\frac{\sqrt{x_1^2+y_1^2}}{h}. $$
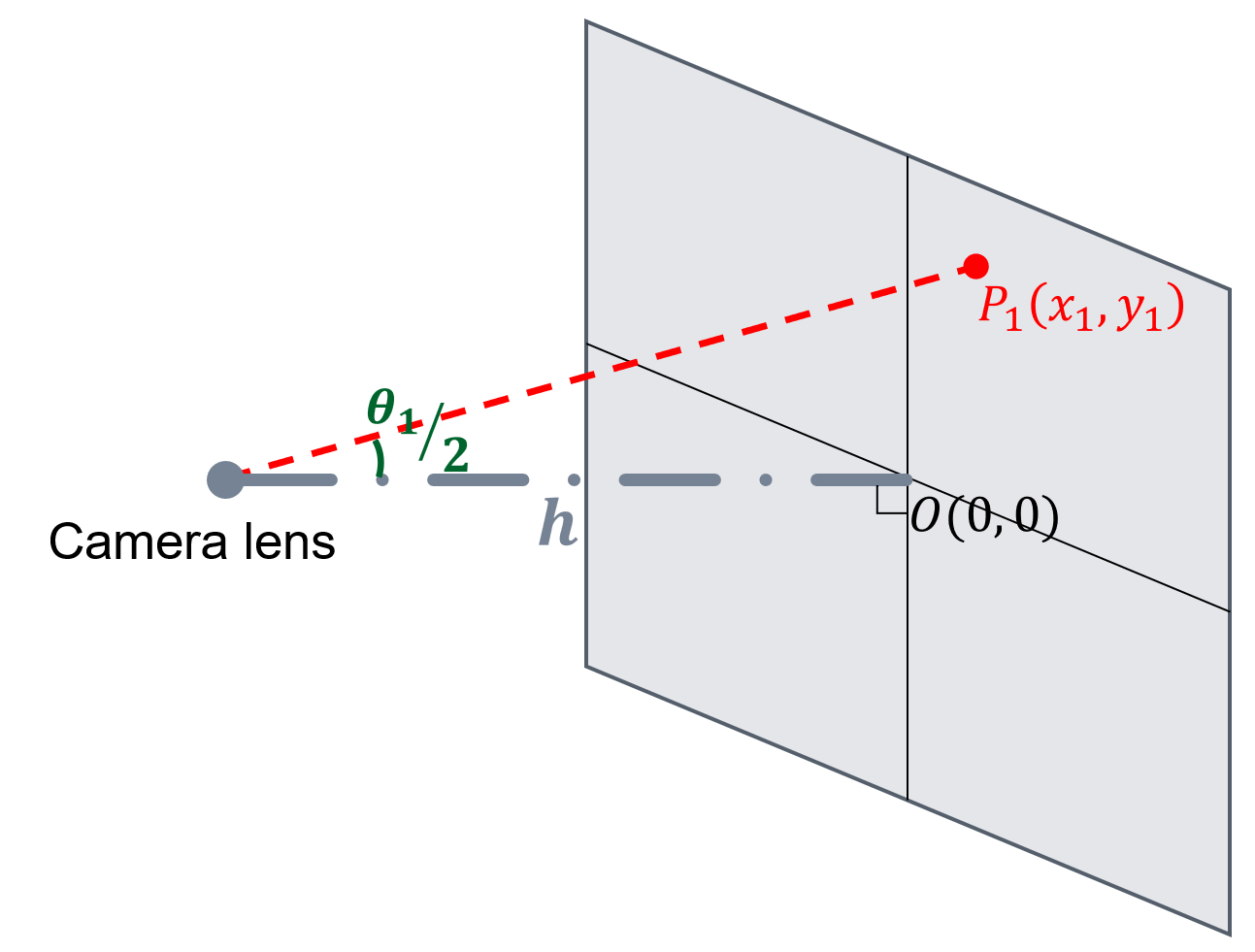
而在成像端,该点在感光芯片上成像像素点相对于中心点的坐标记为$D_1(x_{1d}, y_{1d})$,单位是px。如果认为成像端的像素坐标和角度是成正比的(这一点存疑),那么 $$ \frac{\theta_1/2}{\sqrt{x_{1d}^2+y_{1d}^2}}\equiv K\rm (常数). $$
$$ \therefore ~\tan{\left(K\cdot\sqrt{x_{1d}^2+y_{1d}^2}\right)}=\frac{\sqrt{x_1^2+y_1^2}}{h}. $$
在进行图像校正之前,我们先给出参考用的“锚定点”,即成像点像素位置保持不变的点,$P_{0X}(x_0,0)$ ~ $D_{0X}(x_{0d},0)$,$P_{0Y}(0,y_0)$ ~ $D_{0Y}(0,y_{0d})$。经过校正之后,像素点移动到新的位置, $$ \begin{aligned} D_1(x_{1d},y_{1d})&\rightarrow C_1(x_{1c},y_{1c}),\\ D_{0X}(x_{0d},0)&\rightarrow C_{0X}(x_{0c},0),\\ D_{0Y}(0,y_{0d})&\rightarrow C_{0Y}(0,y_{0c}). \end{aligned} $$
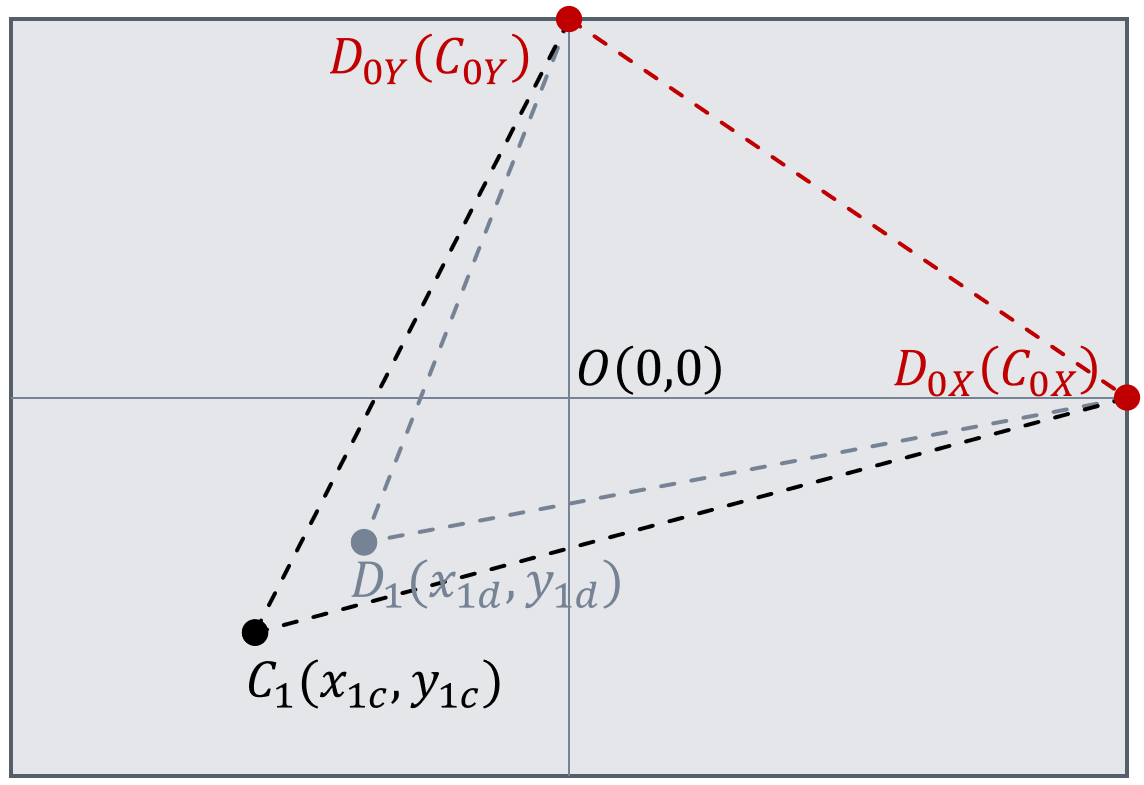
但是“锚定点”事实上位置保持不变,即$x_{0d}=x_{0c},y_{0d}=y_{0c}$。经过校正之后应当满足:$\triangle C_{0X}C_1C_{0Y}$相似于$\triangle P_{0X}P_1P_{0Y}$,或者说$(C_{0X}C_1\parallel{P_{0X}P_1})$且$({C_{0Y}C_1}\parallel{P_{0Y}P_1})$, $$ \displaylines{ \left\{ \begin{aligned} &\frac{x_{1c}-x_{0d}}{y_{1c}-0}=\frac{x_1-x_0}{y_1-0}\\ &\frac{x_{1c}-0}{y_{1c}-y_{0d}}=\frac{x_1-0}{y_1-y_0} \end{aligned} \right. \Rightarrow \left\{ \begin{aligned} &x_{1c}=\frac{(x_1-x_0)y_{0d}+x_{0d}y_1}{x_1y_1-(x_1-x_0)(y_1-y_0)}\\ &y_{1c}=\frac{(y_1-y_0)x_{0d}+x_1y_{0d}}{x_1y_1-(x_1-x_0)(y_1-y_0)} \end{aligned} \right. } $$
通过上述运算,我们现在可以基于给定两个“锚定点”的信息,实现从现实世界中的点坐标到校正后图像坐标的映射$P_1(x_1,y_1)\leftrightarrow C_1(x_{1c},y_{1c})$。通过解(反)三角函数可以得到$P_1\leftrightarrow D_1$的映射,从而构建起图像校正的像素点映射关系$D_1\leftrightarrow C_1$。
📷之后有时间的话,希望能够写成代码检验一下这个算法的适用性🐶