糯米正在看机器学习的网课，我在旁边偷学了一点东西来，感觉还挺有意思的（结果自己的文献都没认真看完😢）

定义

马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的，表示点与一个分布之间的距离，也可以定义为两个服从同一分布并且其协方差矩阵为$\Sigma$的随机变量之间的差异程度¹。马氏距离独立于数据的测量尺度。

根据第一种定义给出的公式： $$ d=\sqrt{ \left(x-\mu\right)’\Sigma^{-1}\left(x-\mu\right) }, $$ 其中$x$是点的向量，$\mu$是分布的均值，$\Sigma$是分布的协方差矩阵。

根据第二种定义给出的公式： $$ d=\sqrt{ \left(x_1-x_2\right)’\Sigma^{-1}\left(x_1-x_2\right) }, $$ 其中$x_1,x_2$是服从同一分布的两个点。

从马氏距离所联想到的

在第一种定义下的马氏距离可以用作“无偏差的假设检验”_{这么描述好像不太准确}——点到不同样本分布的马氏距离可以用于判断该点更可能归属于哪个分布集合。这和假设检验似乎有一些类似的地方，但是不存在对不同假设的偏好差异。

顺带着就复习自学了一下假设检验……_{啥都不记得了，我大学三年到底学了些什么东西？？？}

在传统的假设检验中，原假设$H_0$相较于备择假设$H_1$是更加受到保护的（这里并不强求二者必然形成互补的关系）：当$H_0$条件下的小概率事件发生概率超过阈值(显著性水平)$\alpha$时，$H_0$即被证伪。如果$H_0$和$H_1$分别在这里代表着两种分

布的话，那么有可能$x$虽然处于$H_0$的置信区间内，但是在$H_1$条件下出现$x$事件的概率(密度)更高。这也就会导致第二类错误的发生。

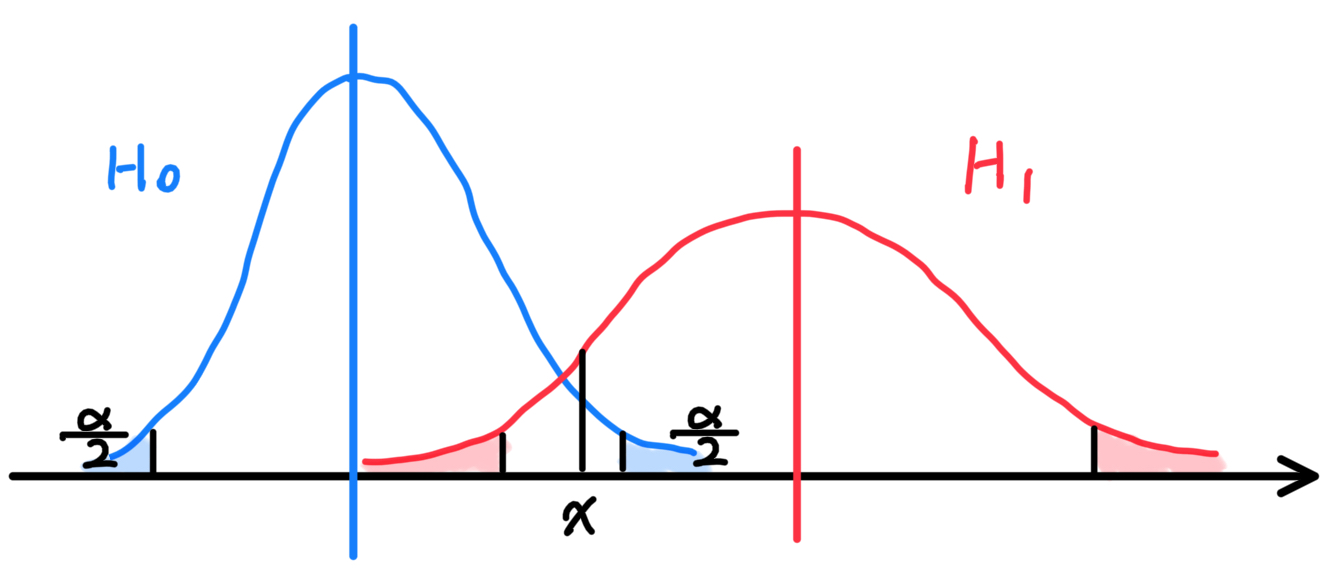
但是在进行马氏距离比较时，则不会面临这一问题。为了和以上描述保持一致，我们这里采用一维变量下的马氏距离公式： $$ d_0=\frac{x-\mu_0}{\sigma_0},~~d_1=\frac{x-\mu_1}{\sigma_1}. $$ 选择$H_0$还是$H_1$完全取决于$d_0$和$d_1$的相对大小，二者的地位是等同的。

但是马氏距离还是不能替代假设检验。即使马氏距离的比较必然能对现有的两个分布做出取舍，但是它并不直接反映出$x$在所选择的分布条件下是否处于置信区间内。马氏距离或许可以用于辅助判断是否发生了第二类错误。

暴力演算

试图把协方差逆矩阵的元素算出来的二哈行为

某$m$维分布的协方差矩阵记为$\Sigma=[c_{ij}]\in R^{m\times m}$，$\Sigma$是对称矩阵，其对角线元素$c_{ii}$是第$i$维上的方差。

协方差逆矩阵$\Sigma^{-1}=[b_{ij}]\in R^{m\times m}$满足： $$ \Sigma \Sigma^{-1}=E_0 $$ 得到约束方程：

$$ c_{1k}b_{k1}+c_{2k}b_{k2}+\dots+c_{mk}b_{km}=1,k\in[1,m] $$

$$ c_{1i}b_{j1}+c_{2i}b_{j2}+\dots +c_{mi}b_{jm}=0,i\neq j,i,j\in[1,m] $$

$$ c_{ij}=c_{ji}, i,j\in[1,m] $$

在$m=2$的简单情形下， $$ \begin{aligned} b_{11}&=\frac{c_{22}}{c_{11}c_{22}-c_{12}^2}\\ b_{22}&=\frac{c_{11}}{c_{11}c_{22}-c_{12}^2}\\ b_{12}=b_{21}&=\frac{c_{12}}{c_{12}^2-c_{11}c_{22}} \end{aligned} $$ 更高纬度的一般性解还没有搞清楚，待以后有空的时候再来研究吧！